
试问:当且仅当a,b满足什么条件时,对椭圆C1:![]() =1(a>b>0)上任意一点P,均存在以P为顶点与圆C0:x2+y2=1外切且与C1内接的平行四边形?证明你的结论。
=1(a>b>0)上任意一点P,均存在以P为顶点与圆C0:x2+y2=1外切且与C1内接的平行四边形?证明你的结论。
解:如图所示,圆外切平行四边形一定是菱形,圆心即菱形中心,所求条件为 必要性的证明: 设椭圆C1上任意一点P(r1cosθ,r1sinθ),所以有Q(r2cos(θ+ 其中|OP|=r1,|OQ|=r2,代入椭圆方程中,得
又菱形PQRS与单位圆C0外切,所以Rt△POQ斜边PQ上的高h=1。而
充分性的证明:设 设|OP|=r1,|OQ|=r2,则P的坐标为(r1cosθ,r1sinθ),Q的坐标为(r2cos(θ+ 代入椭圆方程,得
又在Rt△POQ中,斜边PQ上的高h=1,则h= = ∴ 同理,点O到QR,RS,SP的距离都是1,所以菱形PQRS与单位圆C0外切。 |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:2013年全国高校自主招生数学模拟试卷(九)(解析版) 题型:解答题
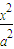 +
+ =1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.
=1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com