
已知椭圆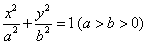 的左焦点为
的左焦点为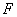
 ,离心率e=
,离心率e=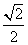 ,M、N是椭圆上的的动点。
,M、N是椭圆上的的动点。
(Ⅰ)求椭圆标准方程;
(Ⅱ)设动点P满足: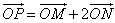 ,直线OM与ON的斜率之积为
,直线OM与ON的斜率之积为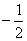 ,问:是否存在定点
,问:是否存在定点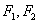 ,使得
,使得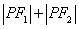 为定值?,若存在,求出
为定值?,若存在,求出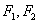 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
(Ⅲ)若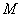 在第一象限,且点
在第一象限,且点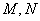 关于原点对称,点
关于原点对称,点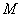 在
在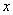 轴上的射影为
轴上的射影为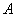 ,连接
,连接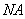 并延长交椭圆于点
并延长交椭圆于点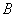 ,证明:
,证明: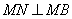 ;
;
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
.某名学生在连续五次考试中数学成绩与物理成绩如下:
| 数学( | 70 | 75 | 80 | 85 | 90 |
| 物理( | 60 | 65 | 70 | 75 | 80 |
(Ⅰ)用茎叶图表示数学成绩与物理成绩;
(Ⅱ)数学成绩为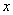 ,物理成绩为
,物理成绩为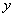 ,求变量
,求变量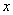 与
与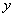 之间的回归直线方程.
之间的回归直线方程.
(注: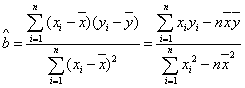 ,
, )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
将 五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件
五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件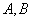 被放在相邻的抽屉内且文件
被放在相邻的抽屉内且文件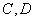 被放在不相邻的抽屉内的概率是 。
被放在不相邻的抽屉内的概率是 。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ex-1,g(x)=-x2+4x-3.若有f(a)=g(b),则b的取值范围为( ).
A.[2-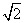 ,2+
,2+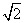 ] B.(2-
] B.(2-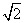 ,2+
,2+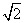 )
)
C.[1,3] D.(1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com