
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
分析 (1)(i)若花店在某一天购进16枝玫瑰花,由当天只卖了14枝,能求出该花店当天的利润为多少元.
(ii)当n≥16时,求出利润,当n≤15时,求出利润,由此能求出当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)X的可能取值为60,70,80,分别求出相应的概率,由此能求出X的分布列和EX.
解答 (本小题满分12分)
解(1)(i)若花店在某一天购进16枝玫瑰花,
则该花店当天的利润为14×(10-5)-2×5=60元.(2分)
(ii)当n≥16时,y=16×(10-5)=80,(3分)
当n≤15时,y=5n-5(16-n)=10n-80,(4分)
得:y=$\left\{\begin{array}{l}{10n-80(n≤15)}\\{80(n≥16)}\end{array}\right.$,n∈N.(5分)
(2)X的可能取值为60,70,80,(6分)
P(X=60)=0.1,
P(X=70)=0.2,
P(X=80)=0.7,(9分)
X的分布列为:
| X | 60 | 70 | 80 |
| P | 0.1 | 0.2 | 0.7 |
点评 本题考查利润、函数解析式、离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
| 日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
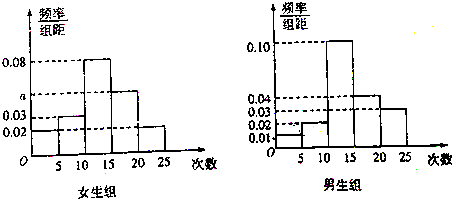
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-2015} | B. | {x|x<-2015} | C. | {x|-2015<x<-2011} | D. | {x|-2011<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com