
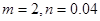
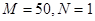 ;(2)见解析;
;(2)见解析;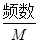 =概率求出M,进一步得出m,n,N即可.
=概率求出M,进一步得出m,n,N即可. ,完成频率分布直方图.
,完成频率分布直方图.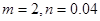
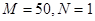 …………4分(2)…………7分
…………4分(2)…………7分

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源:不详 题型:解答题
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
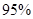 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?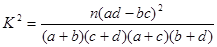 ,其中
,其中 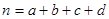
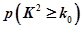 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
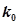 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
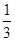 ,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量
,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量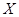 、停留的总时间为变量
、停留的总时间为变量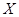 ,
,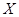 的标准差
的标准差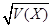 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.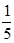 | B.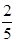 | C.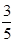 | D.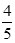 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

A.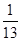 | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
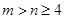 ,现从中任取两球,若取出的两球是同色的概率等于取出的两球是异色的概率,则满足关系
,现从中任取两球,若取出的两球是同色的概率等于取出的两球是异色的概率,则满足关系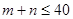 的数组
的数组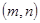 的个数为( )
的个数为( ) | A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com