
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{{x^2}+2}}{{\sqrt{{x^2}+1}}}$ | D. | y=x+$\frac{1}{x-1}$(x>1) |
分析 根据基本不等式的使用条件,即可得出结论.
解答 解:x>0时,y=x+$\frac{1}{x}$的最小值是2,故A不正确;
x∈(0,$\frac{π}{2}$),0<sinx<1,函数取不到2,故B不正确;
y=$\frac{{{x^2}+2}}{{\sqrt{{x^2}+1}}}$=$\sqrt{{x}^{2}+1}$+$\frac{1}{\sqrt{{x}^{2}+1}}$≥2,x=0时取等号,即函数的最小值是2,故正确;
x>1,x-1>0,则y=x+$\frac{1}{x-1}$=x-1+$\frac{1}{x-1}$+1≥2+1,x=02取等号,即函数的最小值是3,故不正确;
故选:C.
点评 本题考查基本不等式的运用,考查学生的计算能力,注意基本不等式的使用条件是关键.


科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{3π}{4}$个单位,再将所得图象上每点纵坐标不变,横坐标变为原来的2倍 | |
| B. | 向左平移$\frac{3π}{4}$个单位,再将所得图象上每点纵坐标不变,横坐标变为原来的2倍 | |
| C. | 每点纵坐标不变,横坐标变为原来的2倍,再将所得图象向右平移$\frac{3π}{4}$个单位 | |
| D. | 每点纵坐标不变,横坐标变为原来的2倍,再将所得图象向左平移$\frac{3π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
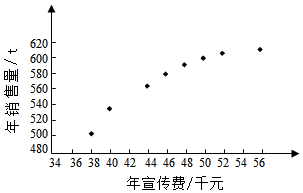
| $\overline x$ | $\overline y$ | $\overline w$ | $\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^8{({x_i}-\overline x)•({{y_i}-\overline y})}$ | $\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}•({{y_i}-\overline y})$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1 469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抽签法 | B. | 随机数法 | C. | 系统抽样法 | D. | 分层抽样法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com