
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由a=${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx利用微积分的几何意义:a表示的是单位圆的面积的$\frac{1}{4}$,可得a.函数y=cos2ax-sin2ax=cos2ax,其周期T=$\frac{2π}{|2a|}$=$\frac{π}{|a|}$=4,解得a,即可判断出关系.
解答 解:利用微积分的几何意义知,a=${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx表示的是单位圆的面积的$\frac{1}{4}$,因此a=$\frac{π}{4}$.
函数y=cos2ax-sin2ax=cos2ax,其周期T=$\frac{2π}{|2a|}$=$\frac{π}{|a|}$=4,解得a=$±\frac{π}{4}$.
∴“a=${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx”是“函数y=cos2ax-sin2ax的最小正周期为4”的充分非必要条件.
故选:A.
点评 本题考查了微积分基本定理、三角函数的图象与性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
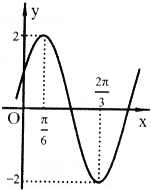 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示:
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{7π}{6}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{{x^2}+2}}{{\sqrt{{x^2}+1}}}$ | D. | y=x+$\frac{1}{x-1}$(x>1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在α∈(0,$\frac{π}{2}$),使sinα+cosα=$\frac{1}{3}$ | |
| B. | y=tanx在其定义域内为增函数 | |
| C. | y=cos2x+sin($\frac{π}{2}$-x)既有最大、最小值,又是偶函数 | |
| D. | y=sin|2x+$\frac{π}{6}$|的最小正周期为π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $3\sqrt{2}$ | C. | $2\sqrt{7}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com