
分析 (1)由已知利用同角三角函数基本关系式可求cosα,tanα的值,利用两角和的正切函数公式可求tan(α+β)的值,结合范围α+β∈(0,π),即可得解α+β的值;
(2)由已知利用同角三角函数基本关系式可求sinβ,cosβ的值,由(1)可知α+2β=$\frac{π}{4}+β$,利用两角和的余弦函数公式即可计算得解.
解答 解:(1)因为α为锐角,且$sinα=\frac{{\sqrt{26}}}{26}$,
所以$cosα=\frac{{5\sqrt{26}}}{26}$,$tanα=\frac{1}{5}$,
因为$tan(α+β)=\frac{tanα+tanβ}{1-tanαtanβ}=\frac{{\frac{1}{5}+\frac{2}{3}}}{{1-\frac{1}{5}×\frac{2}{3}}}=1$,
又因为α+β∈(0,π),
所以$α+β=\frac{π}{4}$.
(2)因为β为锐角,且$tanβ=\frac{2}{3}$,
所以$sinβ=\frac{{2\sqrt{13}}}{13}$,$cosβ=\frac{{3\sqrt{13}}}{13}$,
所以$cos(α+2β)=cos(β+\frac{π}{4})=cosβcos\frac{π}{4}-sinβsin\frac{π}{4}=\frac{{3\sqrt{13}}}{13}×\frac{{\sqrt{2}}}{2}-\frac{{2\sqrt{13}}}{13}×\frac{{\sqrt{2}}}{2}=\frac{{\sqrt{26}}}{26}$.
点评 本题主要考查了同角三角函数基本关系式,两角和的正切函数公式,两角和的余弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱A1B1的中点,点Q在侧面DCC1D1内运动,给出下列结论:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱A1B1的中点,点Q在侧面DCC1D1内运动,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
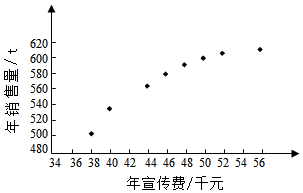
| $\overline x$ | $\overline y$ | $\overline w$ | $\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^8{({x_i}-\overline x)•({{y_i}-\overline y})}$ | $\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}•({{y_i}-\overline y})$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1 469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抽签法 | B. | 随机数法 | C. | 系统抽样法 | D. | 分层抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$+$\frac{3}{2}$i | B. | $\frac{1}{2}$-$\frac{3}{2}$i | C. | -$\frac{1}{2}$-$\frac{3}{2}$i | D. | $\frac{1}{2}$+$\frac{3}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com