
 ��ͼ�����ⳤΪ1��������ABCD-A1B1C1D1�У�PΪ��A1B1���е㣬��Q�ڲ���DCC1D1���˶����������н��ۣ�
��ͼ�����ⳤΪ1��������ABCD-A1B1C1D1�У�PΪ��A1B1���е㣬��Q�ڲ���DCC1D1���˶����������н��ۣ����� ������ͼ��ʾ������ϵ���ֱ������Ӧ�Ĺ켣���̣����ɵó����ۣ�
��� 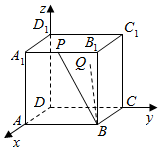 �⣺������ͼ��ʾ������ϵ����A1��1��0��1����C��0��1��0����B��1��1��0����Q��0��y��z����0��y��1��0��z��1��$\overrightarrow{BQ}$=��-1��y-1��z��
�⣺������ͼ��ʾ������ϵ����A1��1��0��1����C��0��1��0����B��1��1��0����Q��0��y��z����0��y��1��0��z��1��$\overrightarrow{BQ}$=��-1��y-1��z��
����BQ��A1C����-1��y-1��z��•��-1��1��-1��=0����1+y-1-z=0����y-z=0��0��y��1��0��z��1����
��Q�Ĺ켣���߶Σ���ȷ��
����|BQ|=$\sqrt{2}$����1+��y-1��2+z2=2���ࣨy-1��2+z2=1��0��y��1��0��z��1����
�ද��Q�Ĺ켣��Բ��һ���֣���ȷ��
��Q����BΪ���㣬BD1Ϊ�Գ��ᣬPQΪֱ����ԲΪ�����Բ��ƽ��CC1D1D�Ľ����ϣ�һ��ĸ��ΪBP����BP��ƽ��CC1D1D��֪��Բĸ��ƽ�е�ƽ���Բ�õ����������ߵ�һ���֣�����ȷ��
������Q��AB��DD1�ľ�����ȣ���y=$\sqrt{1+{z}^{2}}$����y2-z2=1��
�ද��Q�Ĺ켣��˫���ߵ�һ���֣�����ȷ��
�ʴ�Ϊ���٢ڣ�
���� ���⿼��켣���̣�����ѧ����������������������ȷ��������ϵ���ǹؼ���


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��3n | B�� | 4����$\frac{1}{3}$��n | C�� | $\frac{1}{3}$����$\frac{4}{3}$��n-1 | D�� | $\frac{1}{3}$����$\frac{4}{3}$��n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
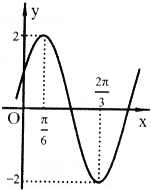 ����f��x��=Asin����x+�գ����أ�0��|��|��$\frac{��}{2}$������ͼ����ͼ��ʾ��
����f��x��=Asin����x+�գ����أ�0��|��|��$\frac{��}{2}$������ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 0 | D�� | ��c�й� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
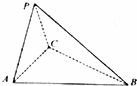 ��ͼ��������P-ABC�У�ƽ��PAC��ƽ��ABC����PAC�ǵȱ������Σ���֪BC=2AC=4��AB=2$\sqrt{5}$��
��ͼ��������P-ABC�У�ƽ��PAC��ƽ��ABC����PAC�ǵȱ������Σ���֪BC=2AC=4��AB=2$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
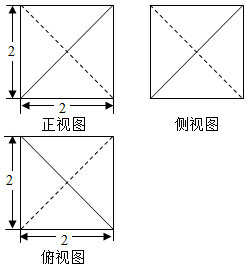
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 8 | C�� | 12 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com