
分析 (1)由椭圆可得:$\left\{\begin{array}{l}{2c=2}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,联立解出即可得出.
(2)设B(x0,y0),则A(x0,-y0).直线PB的方程为:y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),与椭圆T的方程联立可得:(3-2x0)x2-$4{y}_{0}^{2}$x-3${x}_{0}^{2}$+4x0=0.利用根与系数的关系可得:x0xE=$\frac{-3{x}_{0}^{2}+4{x}_{0}}{3-2{x}_{0}}$,可得xE,代入直线方程可得:yE.于是kAE.得出直线AE的方程即可证明.
解答 (1)解:由椭圆可得:$\left\{\begin{array}{l}{2c=2}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,
联立解得a2=2,b2=1,c=1.
∴椭圆T的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)证明:设B(x0,y0),则A(x0,-y0).
直线PB的方程为:y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),与椭圆T的方程联立可得:(3-2x0)x2-$4{y}_{0}^{2}$x-3${x}_{0}^{2}$+4x0=0.
∴x0xE=$\frac{-3{x}_{0}^{2}+4{x}_{0}}{3-2{x}_{0}}$,可得xE=$\frac{3{x}_{0}-4}{2{x}_{0}-3}$,代入直线方程可得:yE=$\frac{-{y}_{0}}{2{x}_{0}-3}$.
∴kAE=$\frac{\frac{-{y}_{0}}{2{x}_{0}-3}-(-{y}_{0})}{\frac{3{x}_{0}-4}{2{x}_{0}-3}-{x}_{0}}$=$\frac{-{y}_{0}}{{x}_{0}-1}$.
∴直线AE的方程为:y+y0=$\frac{-{y}_{0}}{{x}_{0}-1}$(x-x0).
整理为:y=$\frac{-{y}_{0}}{{x}_{0}-1}(x-1)$.
可得直线AE经过定点(1,0).
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、直线方程,考查了推理能力与计算能力,属于难题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:解答题
 某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:
某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:| 分组 | A | B | C |
| 用电量 | (0,80] | (80,250] | (250,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N=U | B. | M∩N=N | C. | M∩(∁UN)=∅ | D. | M⊆∁UN |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 不存在这样的三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{3π}{4}$个单位,再将所得图象上每点纵坐标不变,横坐标变为原来的2倍 | |
| B. | 向左平移$\frac{3π}{4}$个单位,再将所得图象上每点纵坐标不变,横坐标变为原来的2倍 | |
| C. | 每点纵坐标不变,横坐标变为原来的2倍,再将所得图象向右平移$\frac{3π}{4}$个单位 | |
| D. | 每点纵坐标不变,横坐标变为原来的2倍,再将所得图象向左平移$\frac{3π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱A1B1的中点,点Q在侧面DCC1D1内运动,给出下列结论:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱A1B1的中点,点Q在侧面DCC1D1内运动,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
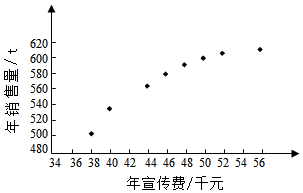
| $\overline x$ | $\overline y$ | $\overline w$ | $\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^8{({x_i}-\overline x)•({{y_i}-\overline y})}$ | $\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}•({{y_i}-\overline y})$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1 469 | 108.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com