
| A. | 4×3n | B. | 4×($\frac{1}{3}$)n | C. | $\frac{1}{3}$×($\frac{4}{3}$)n-1 | D. | $\frac{1}{3}$×($\frac{4}{3}$)n |
分析 利用递推关系与等比数列的通项公式可得an,再利用等差数列的性质可得bn.
解答 解:∵Sn=3-$\frac{1}{2}$an,
∴a1=S1=3-$\frac{1}{2}{a}_{1}$,解得a1=2.
n≥2时,an=Sn-Sn-1=3-$\frac{1}{2}$an-$(3-\frac{1}{2}{a}_{n-1})$,化为:an=$\frac{1}{3}{a}_{n-1}$.
∴数列{an}是等比数列,首项为2,公比为$\frac{1}{3}$.
∴an=$2×(\frac{1}{3})^{n-1}$.
∵bn是an与an+1的等差中项,
∴bn=$\frac{1}{2}$(an+an+1)=$\frac{1}{2}[2×(\frac{1}{3})^{n-1}+2×(\frac{1}{3})^{n}]$=$4×(\frac{1}{3})^{n}$.
故选:B.
点评 本题考查了等差数列与等比数列的通项公式及其性质、递推关系,考查了推理能力与计算能力,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:解答题
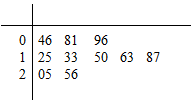 某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:
某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:| 分组 | A | B | C |
| 用电量 | (0,80] | (80,250] | (250,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
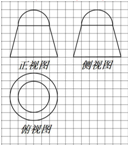
| A. | 17π | B. | 20π | C. | 22π | D. | $(17+5\sqrt{17})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1] | B. | (-∞,$\frac{1}{2}$]∪[1,+∞) | C. | [-$\frac{1}{2}$,1] | D. | (-∞,-$\frac{1}{2}$)∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱A1B1的中点,点Q在侧面DCC1D1内运动,给出下列结论:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为棱A1B1的中点,点Q在侧面DCC1D1内运动,给出下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com