分析:(1)连接BE,由已知中DC=2AD=2AB,AD⊥DC,我们易得四边形DABE为正方形,进而可证得四边形A
1D
1EB为平行四边形,则D
1E∥A
1B,由线面平行的判定定理,可得D
1E∥平面A
1BD;
(2)以D为原点,DA,DC,DD
1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,设DA=1,求出平面A
1BD的一个法向量和平面C
1BD的一个法向量,代入向量夹角公式,即可得到二面角A
1-BD-C
1的余弦值.
(3)由(2)中的平面A
1BD的一个法向量,代入点到平面距离公式
d=,即可求出点C到面A
1BD的距离.
解答:证明:(1)连接BE,则四边形DABE为正方形,
∴BE=AD=A
1D
1,且BE∥AD∥A
1D
1,
∴四边形A
1D
1EB为平行四边形,∴D
1E∥A
1B.
∵D
1E?平面A
1BD,A
1B?平面A
1BD,∴D
1E∥平面A
1BD.
解:(2)以D为原点,DA,DC,DD
1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,不妨设DA=1,
则D(0,0,0),A(1,0,0),B(1,1,0),C
1(0,2,2),A
1(1,0,2).
∴
=(1,0,2),=(1,1,0).
设
=(x,y,z)为平面A
1BD的一个法向量,
由
⊥,⊥得
,取z=1,则
=(-2,-2,1).
设
=(x1,y1,z1)为平面C
1BD的一个法向量,
由
⊥,⊥得
,取z
1=1,则
=(1,-1,1).
cos<,>===-.
由于该二面角A
1-BD-C
1为锐角,所以所求的二面角A
1-BD-C
1的余弦值为
.
(3)∵C(0,2,0),∴
=(1,-1,0).
∴点C到面A
1BD的距离
d===.
点评:本题考查的知识点是与二面角有关的立体几何综合题,直线与平面平行的判定,点到平面之间的距离,其中(1)的关键是证得D1E∥A1B,(2)、(3)的关键是建立空间坐标系,将二面角问题及点到平面的距离转化为用向量法解答.

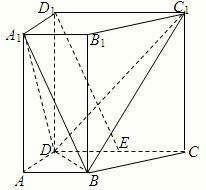 如图,在四棱柱ABCD-A1B1C1D1中,DD1⊥面ABCD已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
如图,在四棱柱ABCD-A1B1C1D1中,DD1⊥面ABCD已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.

 优等生题库系列答案
优等生题库系列答案 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
