
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,证明:
时,证明:![]() ;
;
(Ⅱ)当![]() 时,
时,![]() 恒成立,求正实数
恒成立,求正实数![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ)1.
【解析】
试题分析:(Ⅰ)令![]() ,然后求其导函数,再根据导函数的结构特点构造新函数,从而通过求导研究新函数的单调性,进而使问题得证;(Ⅱ)首先将问题转化为
,然后求其导函数,再根据导函数的结构特点构造新函数,从而通过求导研究新函数的单调性,进而使问题得证;(Ⅱ)首先将问题转化为![]() 对于任意
对于任意![]() 恒成立,从而令
恒成立,从而令![]() ,然后求出其导函数,再根据导函数的结构特点构造新函数,通过求导研究新函数的单调性,进而得到
,然后求出其导函数,再根据导函数的结构特点构造新函数,通过求导研究新函数的单调性,进而得到![]() 的单调性,由此可求得
的单调性,由此可求得![]() 的值.
的值.
试题解析:(Ⅰ)令![]() ,则
,则![]()
令![]() 则
则![]()
![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
![]() 所以
所以![]() 单调递增,
单调递增,
则![]() 即原命题成立.
即原命题成立.
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,
恒成立,
等价于![]() ,对于任意
,对于任意![]() 恒成立,
恒成立,
令![]() ,则
,则![]() .
.
令![]() ,
,
则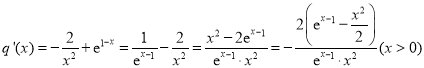 .
.
由(Ⅰ)得![]() ,则
,则![]() 在
在![]() 上单调递减.
上单调递减.
(1)当![]() 时,
时,![]() ,且
,且![]()
在![]() 上
上![]() ,
,![]() 单调递增,在
单调递增,在![]() 上
上![]() ,
,![]() 单调递减,所以
单调递减,所以![]() 的最大值为
的最大值为![]() ,即
,即![]() 恒成立.
恒成立.
(2)当![]() 时,
时,![]() ,
,
![]() 时,由
时,由![]() ,解得
,解得![]() .
.
即![]() 时,
时,![]() ,
,![]() 单调递减,又
单调递减,又![]() ,所以此时
,所以此时![]() ,
,
与![]() 恒成立矛盾.
恒成立矛盾.
(3)当![]() 时,
时,![]() ,
,
![]() 时,由
时,由![]() ,解得
,解得![]() .
.
即![]() 时,
时,![]() ,
,![]() 单调递增,又
单调递增,又![]() ,所以此时
,所以此时![]() ,
,
与![]() 恒成立矛盾.
恒成立矛盾.
综上,![]() 的值为1.
的值为1.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】由与圆心距离相等的两条弦长相等,想到与球心距离相等的两个截面圆的面积相等,用的是( )
A. 三段论推理 B. 类比推理 C. 归纳推理 D. 传递性关系推理
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列给出的输入、输出语句正确的是( )
①输入语句:INPUT a;b;c;
②输入语句:INPUT x=3;
③输出语句:PRINT A=4;
④输出语句:PRINT 20,3*2.
A.①②B.②③
C.③④ D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某珠宝店的一件珠宝被盗,找到了甲、乙、丙、丁4个嫌疑人进行调查.甲说:“我没有偷”;乙说:“丙是小偷”;丙说:“丁是小偷”;丁说:“我没有偷”,若以上4人中只有一人说了真话,只有一人偷了珠宝,那么偷珠宝的人是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视财经频道《升级到家》栏目答题有奖,游戏规则:每个家庭两轮游戏,均为三局两胜,第一轮3题答对2题,可获得小物件(家电),价值1600元;第二轮3题答对2题,可获得大物件(家具)价值5400元(第一轮的答题结果与第二轮答题无关),某高校大二学生吴乾是位孝顺的孩子,决定报名参赛,用自己的知识答题赢取大奖送给父母,若吴乾同学第一轮3题,每题答对的概率均为![]() ,第二轮三题每题答对的概率均为
,第二轮三题每题答对的概率均为![]() .
.
(Ⅰ)求吴乾同学能为父母赢取小物件(家电)的概率;
(Ⅱ)若吴乾同学答题获得的物品价值记为![]() (元)求
(元)求![]() 的概率分布列及数学期望.
的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 及点
及点![]() .
.
(Ⅰ)若线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于
于![]() 两点,试判断四边形
两点,试判断四边形![]() 的形状,并给与证明;
的形状,并给与证明;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙、丙、丁四位学生参加数学竞赛,其中只有一名学生获奖,有其他学生问这四个学生的获奖情况,甲说:“是乙或丙获奖”,乙说:“甲、丙都没有获奖”,丙说:“我获奖了”,丁说:“是乙获奖了”,四位学生的话有且只有两个人的话是对的,则获奖的学生是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com