
已知抛物线的顶点在原点,焦点在x轴的正半轴上,若抛物线的准线与双曲线5x2-y2=20的两条渐近线围成的三角形的面积等于4 ,则抛物线的方程为( )
,则抛物线的方程为( )
(A)y2=4x (B)x2=4y
(C)y2=8x (D)x2=8y
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,已知椭圆C1:  +
+ =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,设P是抛物线C1:x2=y上的动点,过点P作圆C2:x2+(y+3)2=1的两条切线,交直线l:y=-3于A、B两点.

(1)求圆C2的圆心M到抛物线C1准线的距离;
(2)是否存在点P,使线段AB被抛物线C1在点P处的切线平分?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
点A是抛物线C1:y2=2px(p>0)与双曲线C2:  -
- =1(a>0,b>0)的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线C2的离心率等于( )
=1(a>0,b>0)的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线C2的离心率等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源: 题型:
现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众.报告会结束后,为了听取意见,需要请32名听众进行座谈.
③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.
较为合理的抽样方法是( )
A.①简单随机抽样,②系统抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①系统抽样,②简单随机抽样,③分层抽样
D.①分层抽样,②系统抽样,③简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
某地有居民100 000户,其中普通家庭99 000户,高收入家庭1 000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取100户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收入家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700],由于工作中不慎将部分数据丢失,现有以下部分图表:

| 分组 | [100,200] | (200,300] | (300,400] | (400,500] | (500,600] | (600,700] |
| 频数 | B | 30 | E | F | 20 | H |
| 频率 | C | D | 0.2 | 0.4 | G | I |
(1)求图2中的A及表格中的B,C,D,E,F,G,H,I的值;
(2)求图2中阴影部分的面积;
(3)若电子元件的使用时间超过300h为合格产品,求这批电子元件合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
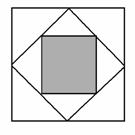
任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了3个正方形,如图所示.若向图形中随机投一点,则所投点落在第三个正方形中的概率是( )
A.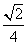 B.
B.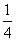
C.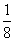 D.
D.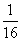
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com