
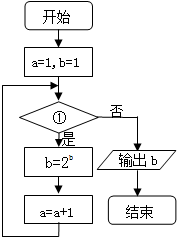
 已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量b的值,并输出,模拟程序的运行,对程序运行过程中各变量的值进行分析,不难得到输出结果.
解答 解:a=1时进入循环,此时b=21=2,a=2时,
再进入循环此时b=22=4,a=3,
再进入循环此时b=24=16,
∴a=4时应跳出循环,
∴循环满足的条件为a≤3?
∴故选:C.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 计算1+21+22+…+210的和 | B. | 计算1+21+22+…+29的和 | ||
| C. | 计算1+3+7+…+(29-1)的和 | D. | 计算1+3+7+…+(210-1)的和 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
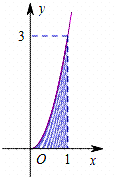 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )| A. | $\frac{99}{100}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com