
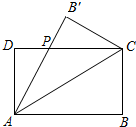
 春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.
春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.分析 (1)AB=x,BC=2-x.因x>2-x,故1<x<2,设DP=y,则PC=x-y.运用三角形全等,结合勾股定理,可得y的关系式;
(2)记△ADP的面积为S1,则S1=(1-$\frac{1}{x}$)(2-x),运用基本不等式可得最大值,即有长与宽.
解答 解:(1)由题意,AB=x,BC=2-x.因x>2-x,故1<x<2,
设DP=y,则PC=x-y.
因△ADP≌△CB'P,故PA=PC=x-y.
由 PA2=AD2+DP2,得(x-y)2=(2-x)2+y2,
即有y=2(1-$\frac{1}{x}$),1<x<2,
(2)记△ADP的面积为S1,则
S1=(1-$\frac{1}{x}$)(2-x)=3-(x+$\frac{2}{x}$)≤3-2$\sqrt{2}$,
当且仅当x=$\sqrt{2}$∈(1,2)时,S1取得最大值.
故设计薄板的长为$\sqrt{2}$,宽为2-$\sqrt{2}$时,最节能.
点评 本题考查函数的最值的求法,注意根据题意求出面积函数的解析式,运用基本不等式,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com