
分析 (1)利用递推关系取n=1,2,3即可得出.
(2)利用数列递推关系即可得出.
(3)利用放缩与“裂项求和”方法即可得出.
解答 (1)解:令n=1,得a1=1;令n=2,有a1+2a2=2,得${a_2}=\frac{1}{2}$;
令n=3,有${a_1}+2{a_2}+3{a_3}=\frac{11}{4}$,得${a_3}=\frac{1}{4}$.
(2)解:∵${a_1}+2{a_2}+…+n{a_n}=4-\frac{n+2}{{{2^{n-1}}}}$,(1)式
所以,当n≥2时,${a_1}+2{a_2}+…+(n-1){a_{n-1}}=4-\frac{n+1}{{{2^{n-2}}}}$,(2)式
两式相减得:$n{a_n}=\frac{n+1}{{{2^{n-2}}}}-\frac{n+2}{{{2^{n-1}}}}=\frac{n}{{{2^{n-1}}}}$,∴${a_n}=\frac{1}{{{2^{n-1}}}}$.
当n=1时,a1=1也适合${a_n}=\frac{1}{{{2^{n-1}}}}$,
∴${a_n}=\frac{1}{{{2^{n-1}}}}$(n∈N*).
(3)证明:${b_n}=1+{log_{\frac{1}{2}}}{a_n}=1+{log_{\frac{1}{2}}}\frac{1}{{{2^{n-1}}}}=n$,
当n=1时,$\frac{1}{b_1^2}=1<\frac{7}{4}$;当n=2时,$\frac{1}{b_1^2}+\frac{1}{b_2^2}=1+\frac{1}{4}=\frac{5}{4}<\frac{7}{4}$;
当n>2时,$\frac{1}{b_n^2}=\frac{1}{n^2}<\frac{1}{n(n-1)}=\frac{1}{n-1}-\frac{1}{n}$,$\frac{1}{b_1^2}+\frac{1}{b_2^2}+…+\frac{1}{b_n^2}<\frac{1}{b_1^2}+\frac{1}{b_2^2}+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n-1}-\frac{1}{n})=1+\frac{1}{4}+\frac{1}{2}-\frac{1}{n}=\frac{7}{4}-\frac{1}{n}<\frac{7}{4}$,
综合可得:$\frac{1}{b_1^2}+\frac{1}{b_2^2}+…+\frac{1}{b_n^2}<\frac{7}{4}$.
点评 本题考查了数列递推关系、放缩法与“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
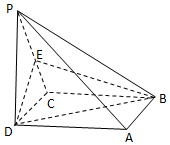 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $arcsin\frac{1}{3}$ | B. | $-\frac{π}{2}-arcsin(-\frac{1}{3})$ | C. | $-π+arcsin(-\frac{1}{3})$ | D. | $-π-arcsin(-\frac{1}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com