
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3 ![]() ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣ ![]() .
.
(1)求a和sinC的值;
(2)求cos(2A+ ![]() )的值.
)的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( ) 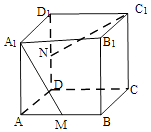
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正三棱锥P﹣ABC中,CM=2PM,CN=2NB,对于以下结论:
①二面角B﹣PA﹣C大小的取值范围是( ![]() ,π);
,π);
②若MN⊥AM,则PC与平面PAB所成角的大小为 ![]() ;
;
③过点M与异面直线PA和BC都成 ![]() 的直线有3条;
的直线有3条;
④若二面角B﹣PA﹣C大小为 ![]() ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成 ![]() 的直线有3条.
的直线有3条.
正确的序号是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′= ![]() ,连接CC′,E为CC′的中点.
,连接CC′,E为CC′的中点. 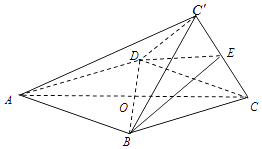
文科:
(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .建立如图所示的空间直角坐标系.
.建立如图所示的空间直角坐标系.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆方程:
(1)长轴在x轴上,长轴长等于12,离心率等于 ![]() ;
;
(2)椭圆经过点(﹣6,0)和(0,8);
(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人 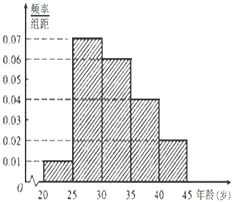
(1)求该组织的人数;
(2)若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com