|
|
|
有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有
|
| [ ] |
A. |
60种
|
B. |
70种
|
C. |
75种
|
D. |
150种
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人教B版(新课标) 必修5
题型:
|
|
|
在△ABC中,已知a=8,B=60°,C=75°,则b等于
|
| [ ] |
A. |
4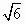
|
B. |
4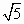
|
C. |
4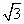
|
D. |
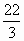
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教A版(新课标) 选修4-1 几何证明选讲
题型:
|
|
|
在△ABC中,sinA=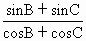 ,判断△ABC的形状并证明. ,判断△ABC的形状并证明.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设△ABC的内角A,B,C所对边的长分别是a,b,c,且b=3,c=1,A=2B.
(1)求a的值;
(2)求sin(A+ )的值. )的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知角α的终边经过点(-4,3),则cosα=
|
| [ ] |
A. |
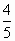
|
B. |
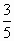
|
C. |
-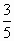
|
D. |
-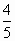
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
奇函数f(x)的定义域为R,若f(x+2)为偶函数,则f(1)=1,则f(8)+f(9)=
|
| [ ] |
A. |
-2
|
B. |
-1
|
C. |
0
|
D. |
1
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为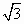 ,求二面角A1-AB-C的大小. ,求二面角A1-AB-C的大小.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若三角形 ABC的内角满足sinA+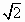 sinB=2sinC,则cosC的最小值是________. sinB=2sinC,则cosC的最小值是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若变量x,y满足约束条件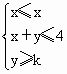 ,且z=2x+y的最小值为-6,则k=________. ,且z=2x+y的最小值为-6,则k=________.
|
|
|
查看答案和解析>>
