
设F1、F2分别是椭圆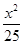 +
+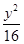 =1的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______
=1的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______
15
解析试题分析:因为设F1、F2分别是椭圆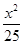 +
+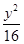 =1的左、右焦点,由于a=5,b=4,那么c=3,根据第一可知焦点的坐标为(3,0)(-3,0),而点M的坐标为(6,4)的坐标在椭圆外,那么连接MF则此时距离和最小,但是要使得最大,则所求的转换为|PM|+2a-|PF2|=2a+|PM|-|PF2|,可知连接左焦点和点M的线段的连线即为|PM|-|PF2|的最大值为5,那么|PM|+|PF1|的最大值为5+2a=15.故答案为15.
=1的左、右焦点,由于a=5,b=4,那么c=3,根据第一可知焦点的坐标为(3,0)(-3,0),而点M的坐标为(6,4)的坐标在椭圆外,那么连接MF则此时距离和最小,但是要使得最大,则所求的转换为|PM|+2a-|PF2|=2a+|PM|-|PF2|,可知连接左焦点和点M的线段的连线即为|PM|-|PF2|的最大值为5,那么|PM|+|PF1|的最大值为5+2a=15.故答案为15.
考点:本题主要考查了椭圆的应用以及椭圆中线段的最值问题,求解时要充分利用椭圆的定义可使得解答简洁.
点评:解决该试题的关键是将求解线段和的最小值转换为三点共线的特殊情况来解决,结合定义得到。


科目:高中数学 来源: 题型:填空题
若方程 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4; ②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆; ④若 ,则C表是长轴在x轴上的椭圆.
,则C表是长轴在x轴上的椭圆.
其中真命题的序号为 (把所有正确命题的序号都填上)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com