
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2sin θ,θ∈[0,2π).
(1)求曲线C的直角坐标方程;
(2)在曲线C上求一点D,使它到直线l:![]() 的距离最短,并求出点D的直角坐标.
的距离最短,并求出点D的直角坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用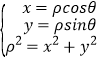 可把圆C的极坐标方程化为普通方程.
可把圆C的极坐标方程化为普通方程.
(2)利用圆的几何性质即可得到结果.
(1)由ρ=2sin θ,θ∈[0,2π),可得ρ2=2ρsin θ.
因为ρ2=x2+y2,ρsin θ=y,
所以曲线C的直角坐标方程为x2+(y-1)2=1.
(2)因为曲线C:x2+(y-1)2=1是以C(0,1)为圆心、1为半径的圆,易知曲线C与直线l相离.
设点D(x0,y0),且点D到直线l:y=-![]() x+5的距离最短,
x+5的距离最短,
所以曲线C在点D处的切线与直线l:y=-![]() x+5平行.
x+5平行.
即直线CD与l的斜率的乘积等于-1,
即![]() ×(-
×(-![]() )=-1,又x+(y0-1)2=1,
)=-1,又x+(y0-1)2=1,
可得x0=-![]() (舍去)或x0=
(舍去)或x0=![]() ,所以y0=
,所以y0=![]() ,
,
即点D的坐标为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是递增的等差数列,且满足a2a4=21,a1+a5=10.
(1)求{an}的通项公式;
(2)若数列{cn}前n项和Cn=an+1,数列{bn}满足bn=2ncn(n∈N*),求{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)若 ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一则“清华大学要求从 2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.其实,已有不少高校将游泳列为必修内容.
某中学拟在高一-下学期开设游泳选修课,为了了解高--学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1).请将上述列联表![]() 补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
(2)已知在被调查的学生中有6名来自高一(1) 班,其中4名喜欢游泳,现从这6名学生中随机抽取2人,求恰有1人喜欢游泳的概率.
附:![]()
| 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 /td> | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 由经验得知,在某商场付款处排队等候付款的人数及概率如下表
排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(1)至多有2人排队的概率是多少?
(2)至少有2人排队的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为( )
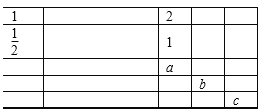
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,且 ![]() 为偶函数,对于函数y=f(x)有下列几种描述:①y=f(x)是周期函数②x=π是它的一条对称轴;③(﹣π,0)是它图象的一个对称中心;④当
为偶函数,对于函数y=f(x)有下列几种描述:①y=f(x)是周期函数②x=π是它的一条对称轴;③(﹣π,0)是它图象的一个对称中心;④当 ![]() 时,它一定取最大值;其中描述正确的是 .
时,它一定取最大值;其中描述正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A=a1 , a2 , a3 , …,an , 其中ai∈R(1≤i≤n,n>2),l(A)表示和ai+aj(1≤i<j≤n)中所有不同值的个数.
(Ⅰ)设集合P=2,4,6,8,Q=2,4,8,16,分别求l(P)和l(Q);
(Ⅱ)若集合A=2,4,8,…,2n , 求证: ![]() ;
;
(Ⅲ)l(A)是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com