
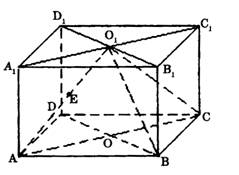
(08年成都七中二模理) 如图,直四棱柱ABCD―A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,
AC∩BD=O,A1C1∩B1D1=O1,E是O1A的中点.
(1)求证:平面O1AC![]() 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离.

解析:(1)∵ABCD为菱形,∴AC⊥BD,又OO1//AA1,AA⊥平面ABCD,
OO1⊥平面ABCD,∴BD⊥OO1,OO1![]() AC=O,
AC=O,
∴BD⊥平面O1AC,平面O1BD⊥平面O1AC……4分
(2)过O作OF⊥BC于F,连接O1F,
∵OO1⊥面AC,∴BC⊥O1F,
∴∠O1FO是二面角O1-BC-D的平面角,
∵OB=2,∠OBF=60°,∴OF=![]() .在Rt△O1OF在,tan∠O1FO=
.在Rt△O1OF在,tan∠O1FO=![]()
∴∠O1FO=60° 即二面角O1―BC―D为60°……8分
(3)在△O1AC中,OE是△O1AC的中位线,∴OE∥O1C
∴OE∥O1BC,∵BC⊥面O1OF,∴面O1BC⊥面O1OF,交线O1F.
过O作OH⊥O1F于H,则OH是点O到面O1BC的距离,
∴OH=![]() ∴点E到面O1BC的距离等于
∴点E到面O1BC的距离等于![]() ……12分
……12分
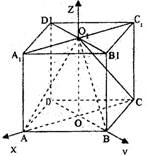
解法二:(2)∵OO1⊥平面AC,∴OO1⊥OA,OO1⊥OB,
又OA⊥OB,建立如图所示的空间直角坐标系(如图)
∵底面ABCD是边长为4,∠DAB=60°的菱形,
∴OA=2![]() ,OB=2,则A(2
,OB=2,则A(2![]() ,0,0),B(0,2,0),
,0,0),B(0,2,0),
C(-2![]() ,0,0),O1(0,0,3)
,0,0),O1(0,0,3)
设平面O1BC的法向量为![]() =(x,y,z),
=(x,y,z),
则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ,则z=2,则x=-
,则z=2,则x=-![]() ,y=3,
,y=3,
∴![]() =(-
=(-![]() ,3,2),
,3,2),
而平面AC的法向量![]() =(0,0,3)∴cos<
=(0,0,3)∴cos<![]() ,
,![]() >=
>=![]() ,
,
设O1-BC-D的平面角为α,
∴cosα=![]() ∴α=60°. 故二面角O1-BC-D为60°.
∴α=60°. 故二面角O1-BC-D为60°.
(3)设点E到平面O1BC的距离为d,
∵E是O1A的中点,∴![]() =(-
=(-![]() ,0,
,0,![]() ),
),
则d=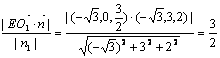 ∴点E到面O1BC的距离等于
∴点E到面O1BC的距离等于![]() 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(08年成都七中二模理) 设甲、乙两套试验方案在一次试验中成功的概率均为p,且这两套试验方案中至少有一套试验成功的概率为0.51. 假设这两套试验方案在试验过程中,相互之间没有影响.
(I)求p的值;(II)设试验成功的方案的个数为![]() ,求
,求![]() 的分布列及数学期望E
的分布列及数学期望E![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年成都七中二模理) 已知圆![]() 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足![]() .
.
(1)求点G的轨迹C的方程;
(2)过点(2,0)作直线![]() ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设![]() 是否存在这样的直线
是否存在这样的直线![]() ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线![]() 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com