
设函数f(x)=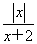 -ax2,a∈R.
-ax2,a∈R.
(1)当a=2时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点;
(3)若函数f(x)有四个不同的零点,求a的取值范围.
(1)0,x=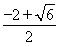 ,x=
,x=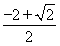 ,x=
,x=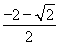 (2)见解析(3)(1,+∞)
(2)见解析(3)(1,+∞)
【解析】(1)【解析】
当x≥0时,由f(x)=0,得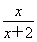 -2x2=0,即x(2x2+4x-1)=0,解得x=0或x=
-2x2=0,即x(2x2+4x-1)=0,解得x=0或x=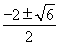 (舍负);
(舍负);
当x<0时,由f(x)=0,得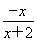 -2x2=0,
-2x2=0,
即x(2x2+4x+1)=0(x≠-2),解得x=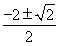 .
.
综上所述,函数f(x)的零点为0,x=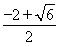 ,x=
,x=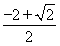 ,x=
,x=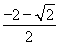 .
.
(2)证明:当a>0且x>0时,由f(x)=0,得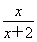 -ax2=0,即ax2+2ax-1=0.
-ax2=0,即ax2+2ax-1=0.
记g(x)=ax2+2ax-1,则函数g(x)的图象是开口向上的抛物线.
又g(0)=-1<0,所以函数g(x)在(0,+∞)内有且仅有一个零点,
即函数f(x)在区间(0,+∞)内有且仅有一个零点.
(3)【解析】
易知0是函数f(x)的零点.
对于x>0,由(2)知,当a>0时,函数f(x)在区间(0,+∞)内有且仅有一个零点;
当a≤0时,g(x)=ax2+2ax-1<0恒成立,因此函数f(x)在区间(0,+∞)内无零点.
于是,要使函数f(x)有四个不同的零点,函数f(x)在区间(-∞,0)内就要有两个不同的零点.
当x<0时,由f(x)=0,得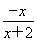 -ax2=0,即ax2+2ax+1=0(x≠-2).①
-ax2=0,即ax2+2ax+1=0(x≠-2).①
因为a=0不符合题意,所以①式可化为x2+2x+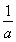 =0(x≠-2),即x2+2x=-
=0(x≠-2),即x2+2x=-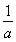 =0.
=0.
作出函数h(x)=x2+2x(x<0)的图象便知-1<-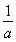 <0,得a>1,
<0,得a>1,
综上所述,a的取值范围是(1,+∞).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
已知集合A={x|33-x<6},B={x|lg(x-1)<1},则A∩B=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:填空题
若函数f(x)=ex-ax在x=1处取到极值,则a=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第11课时练习卷(解析版) 题型:填空题
曲线y=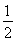 x-cosx在x=
x-cosx在x=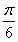 处的切线方程为________.
处的切线方程为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第10课时练习卷(解析版) 题型:填空题
已知函数f(x)= 若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是________.
若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第10课时练习卷(解析版) 题型:解答题
(1)求函数f(x)=x3-2x2-x+2的零点;
(2)已知函数f(x)=ln(x+1)-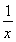 ,试求函数的零点个数.
,试求函数的零点个数.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第9课时练习卷(解析版) 题型:解答题
在△ABC中,角A、B、C对应的边分别是a、b、c.已知cos2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5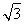 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第9课时练习卷(解析版) 题型:填空题
已知函数f(x)=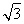 sinxcosx-cos2x+
sinxcosx-cos2x+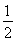 (x∈R),则f(x)在区间
(x∈R),则f(x)在区间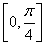 上的值域是________.
上的值域是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第7课时练习卷(解析版) 题型:填空题
在△ABC中,a、b、c分别为角A、B、C所对的边,若a=2bcosC,则此三角形一定是________三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com