
【题目】为了调查各校学生体质健康达标情况,某机构M采用分层抽样的方法从![]() 校抽取了
校抽取了![]() 名学生进行体育测试,成绩按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下频率分布直方图.根据规定,测试成绩低于60分为体质不达标.已知本次测试中不达标学生共有20人.
名学生进行体育测试,成绩按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下频率分布直方图.根据规定,测试成绩低于60分为体质不达标.已知本次测试中不达标学生共有20人.
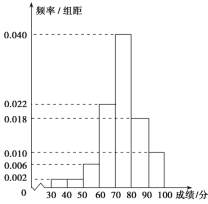
(1)求![]() 的值;
的值;
(2)现从![]() 校全体同学中随机抽取2人,以频率作为概率,记
校全体同学中随机抽取2人,以频率作为概率,记![]() 表示成绩不低于90分的人数,求
表示成绩不低于90分的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)另一机构N也对该校学生做同样的体质达标测试,并用简单随机抽样方法抽取了100名学生,经测试有20名学生成绩低于60分.计算两家机构测试成绩的不达标率,你认为用哪一个值作为对该校学生体质不达标率的估计较为合理,说明理由.
【答案】(1)![]() ;(2)分布列详见解析,数学期望为0.2;(3)用机构M测试的不达标率
;(2)分布列详见解析,数学期望为0.2;(3)用机构M测试的不达标率![]() 估计A校不达标率较为合理,理由详见解析.
估计A校不达标率较为合理,理由详见解析.
【解析】
(1)由频率分布直方图知,![]() ,解方程可得
,解方程可得![]() 的值;
的值;
(2)由图知,每位学生成绩不低于90分的频率为![]() ,由已知
,由已知![]() 的所有可能取值为
的所有可能取值为![]() ,再根据二项分布,即可得答案;
,再根据二项分布,即可得答案;
(3)机构M抽测的不达标率为![]() ,机构N抽测的不达标率为
,机构N抽测的不达标率为![]() ,再从样本能否较好反映总体的分布情况说明理由.
,再从样本能否较好反映总体的分布情况说明理由.
(1)由频率分布直方图知,![]() ,
,
解得![]() .
.
(2)由图知,每位学生成绩不低于90分的频率为![]() ,
,
由已知,![]() 的所有可能取值为
的所有可能取值为![]() ,
,
则![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为
的分布列为
X | 0 | 1 | 2 |
P | 0.81 | 0.18 | 0.01 |
所以![]() .
.
(3)机构M抽测的不达标率为![]() ,
,
机构N抽测的不达标率为![]() .
.
(以下答案不唯一,只要写出理由即可)
①用机构M测试的不达标率![]() 估计A校不达标率较为合理.
估计A校不达标率较为合理.
理由:机构M选取样本时使用了分层抽样方法,样本量也大于机构N,样本更有代表性,所以,能较好反映了总体的分布.
②没有充足的理由否认机构N的成绩更合理.
理由:尽管机构N的样本量比机构M少,但由于样本的随机性,不能排除样本较好的反映了总体的分布,所以,没有充足的理由否认机构N的成绩更合理.


科目:高中数学 来源: 题型:
【题目】有如下命题:①函数y=sinx与y=x的图象恰有三个交点;②函数y=sinx与y=![]() 的图象恰有一个交点;③函数y=sinx与y=x2的图象恰有两个交点;④函数y=sinx与y=x3的图象恰有三个交点,其中真命题的个数为( )
的图象恰有一个交点;③函数y=sinx与y=x2的图象恰有两个交点;④函数y=sinx与y=x3的图象恰有三个交点,其中真命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市旅游局为尽快恢复受疫情影响的旅游业,准备在本市的景区推出旅游一卡通(年卡).为了更科学的制定一卡通的有关条例,市旅游局随机调查了2019年到本市景区旅游的1000个游客的年旅游消费支出(单位:百元),并制成如下频率分布直方图:
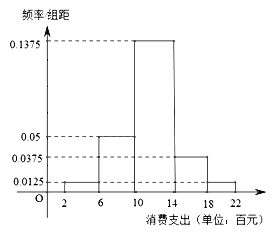
由频率分布直方图,可近似地认为到本市景区旅游的游客,其旅游消费支出服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (同一组数据用该组区间的中点值作代表).
(同一组数据用该组区间的中点值作代表).
(1) 若2019年到本市景区旅游游客为500万人,试估计2019年有多少游客在本市的年旅游消费支出不低于1820元;
(2) 现依次抽取![]() 个游客,假设每个游客的旅游消费支出相互独立,记事件
个游客,假设每个游客的旅游消费支出相互独立,记事件![]() 表示“连续3人的旅游消费支出超出
表示“连续3人的旅游消费支出超出![]() ”.若
”.若![]() 表示
表示![]() 的概率,
的概率,![]() 为常数),且
为常数),且![]() .
.
(ⅰ)求![]() ,
,![]() 及
及![]() ,
,![]() ;
;
(ⅱ)判断并证明数列![]() 从第三项起的单调性,试用概率统计知识解释其实际意义.
从第三项起的单调性,试用概率统计知识解释其实际意义.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分类,是指按一定规定或标准将垃圾分类储存、分类投放和分类搬运,从而转变成公共资源的一系列活动的总称.分类的目的是提高垃圾的资源价值和经济价值,力争物尽其用.2019年6月25日,生活垃圾分类制度入法.到2020年底,先行先试的46个重点城市,要基本建成垃圾分类处理系统;其他地级城市实现公共机构生活垃圾分类全覆盖.某机构欲组建一个有关“垃圾分类”相关事宜的项目组,对各个地区“垃圾分类”的处理模式进行相关报道.该机构从600名员工中进行筛选,筛选方法:每位员工测试![]() ,
,![]() ,
,![]() 三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试
三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试![]() ,
,![]() 两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试
两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试![]() ,
,![]() ,
,![]() 三项工作相互独立,每一项测试“不合格”的概率均为
三项工作相互独立,每一项测试“不合格”的概率均为![]() .
.
(1)记某位员工被认定为“暂定”的概率为![]() ,求
,求![]() ;
;
(2)每位员工不需要重新测试的费用为90元,需要重新测试的总费用为150元,除测试费用外,其他费用总计为1万元,若该机构的预算为8万元,且该600名员工全部参与测试,问上述方案是否会超过预算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是我国古代的天文学和数学著作.其中有一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).二十四个节气及晷长变化如图所示,若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至后的那个节气(小暑)晷长为( )
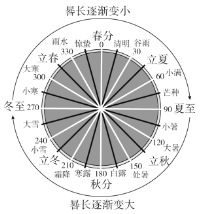
A.五寸B.二尺五寸C.三尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() :
:![]() 右焦点的直线
右焦点的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且椭圆
两点,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 为
为![]() 上的两点,若四边形
上的两点,若四边形![]() 的对角线
的对角线![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种产品的标准长度为![]() ,只要误差的绝对值不超过
,只要误差的绝对值不超过![]() 就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
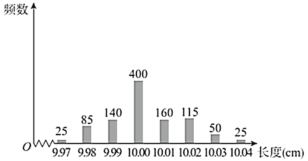
(1)估计该批次产品长度误差绝对值的数学期望;
(2)如果视该批次产品样本的频率为总体的概率,要求从工厂生产的产品中随机抽取2件,假设其中至少有1件是标准长度产品的概率不小于0.8时,该设备符合生产要求.现有设备是否符合此要求?若不符合此要求,求出符合要求时,生产一件产品为标准长度的概率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com