
【题目】有如下命题:①函数y=sinx与y=x的图象恰有三个交点;②函数y=sinx与y=![]() 的图象恰有一个交点;③函数y=sinx与y=x2的图象恰有两个交点;④函数y=sinx与y=x3的图象恰有三个交点,其中真命题的个数为( )
的图象恰有一个交点;③函数y=sinx与y=x2的图象恰有两个交点;④函数y=sinx与y=x3的图象恰有三个交点,其中真命题的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
①构造函数f(x)=sinx-x,求出函数的导数,研究函数的导数和单调性,进行判断即可;
②利用![]() 与x的关系进行转化判断;
与x的关系进行转化判断;
③和④直接作出两个函数的图象即可进行判断.
①设f(x)=sinx-x,则f′(x)=cosx-1≤0,即函数f(x)为减函数,
∵f(0)=0,
∴函数f(x)只有一个零点,即函数y=sinx与y=x的图象恰有一个交点,故①错误,
②由①知当x>0时,sinx<x,
当0<x≤1时,![]() >x>sinx,
>x>sinx,
当x>1时,![]() >sinx,
>sinx,
当x=0时,sinx=![]() ,综上当x>0时,
,综上当x>0时,![]() >sinx恒成立,
>sinx恒成立,
函数y=sinx与y=![]() 的图象恰有一个交点,故②正确,
的图象恰有一个交点,故②正确,
③作出函数y=sinx与y=x2,的图象,由图象知两个函数有2个交点,即函数y=sinx与y=x2的图象恰有两个交点,故③正确,
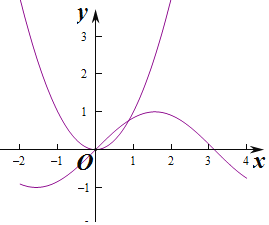
④作出函数y=sinx与y=x3,的图象,由图象知两个函数有3个交点,即函数y=sinx与y=x3的图象恰有三个交点,故④正确,

故正确的是②③④,
故选C.


科目:高中数学 来源: 题型:
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
晷影长 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易经》中记录某年的冬至晷影长为130.0寸,夏至晷影长为14.8寸,按照上述规律那么《易经》中所记录的春分的晷影长应为( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
(θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程以及曲线C2的直角坐标方程;
(2)若直线l:y=kx与曲线C1、曲线C2在第一象限交于P、Q,且|OQ|=|PQ|,点M的直角坐标为(1,0),求△PMQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求证:x1+x2<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 与
与![]() 的交点
的交点![]() 恰好是
恰好是![]() 中点,又
中点,又![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)设![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,若直线
上,若直线![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义![]() 为两点
为两点![]() ,
,![]() 的“切比雪夫距离”,又设点
的“切比雪夫距离”,又设点![]() 及
及![]() 上任意一点
上任意一点![]() ,称
,称![]() 的最小值为点
的最小值为点![]() 到直线
到直线![]() 的“切比雪夫距离”,记作
的“切比雪夫距离”,记作![]() ,给出下列三个命题:
,给出下列三个命题:
①对任意三点![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
②已知点![]() 和直线
和直线![]() :
:![]() ,则
,则![]() ;
;
③到定点![]() 的距离和到
的距离和到![]() 的“切比雪夫距离”相等的点的轨迹是正方形.
的“切比雪夫距离”相等的点的轨迹是正方形.
其中正确的命题有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查各校学生体质健康达标情况,某机构M采用分层抽样的方法从![]() 校抽取了
校抽取了![]() 名学生进行体育测试,成绩按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下频率分布直方图.根据规定,测试成绩低于60分为体质不达标.已知本次测试中不达标学生共有20人.
名学生进行体育测试,成绩按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下频率分布直方图.根据规定,测试成绩低于60分为体质不达标.已知本次测试中不达标学生共有20人.
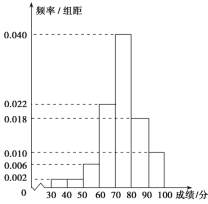
(1)求![]() 的值;
的值;
(2)现从![]() 校全体同学中随机抽取2人,以频率作为概率,记
校全体同学中随机抽取2人,以频率作为概率,记![]() 表示成绩不低于90分的人数,求
表示成绩不低于90分的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)另一机构N也对该校学生做同样的体质达标测试,并用简单随机抽样方法抽取了100名学生,经测试有20名学生成绩低于60分.计算两家机构测试成绩的不达标率,你认为用哪一个值作为对该校学生体质不达标率的估计较为合理,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com