
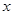 (元/评)与销售量
(元/评)与销售量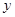 (瓶)的关系统计如下:
(瓶)的关系统计如下:| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
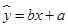 ,其中
,其中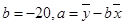 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( ) 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:不详 题型:解答题
| 销售量x(吨) | 2 | 3 | 5 | 6 |
| 销售收入y(千元) | 7 | 8 | 9 | 12 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 甲班: | 158 | 168 | 162 | 168 | 163 | 170 | 182 | 179 | 171 | 179 |
| 乙班: | 159 | 168 | 162 | 170 | 165 | 173 | 176 | 181 | 178 | 179 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.不论采用何种抽样方法,这100个零件中每个被抽到的可能性均为
| ||
B.①、②两种抽样方法,这100个零件中每个被抽到的可能性均为
| ||
C.①、③两种抽样方法,这100个零件中每个被抽到的可能性均为
| ||
| D.采用不同的抽样方法,这100个零件中每个被抽到的可能性是各不相同的 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 0 | 1 | 2 | 3 |
| y | 0 | 2 | 6 | 7 |
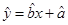 必过点( )
必过点( )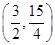 D.(3,7)
D.(3,7)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
月平均气温 (°C) (°C) | 11 | 13 | 12 |
| 月销售量y(件) | 25 | 30 | 26 |
 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
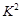 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当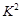 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当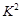 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当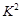
 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的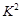 ="20." 87,根据这一数据分析,认为打鼾与患心脏病之间
="20." 87,根据这一数据分析,认为打鼾与患心脏病之间 | A.有95%的把握认为两者有关 |
| B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 |
| D.约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 支持A方案 | 支持B方案 | 支持C方案 |
| 35岁以下 | 200 | 400 | 800 |
| 35岁以上(含35岁) | 100 | 100 | 400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com