
【题目】已知![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosφ,sinφ)(|φ|<
=(cosφ,sinφ)(|φ|<![]() ).函数
).函数
f(x)=![]()
![]() 且f(
且f(![]() -x)=f(x).
-x)=f(x).
(Ⅰ)求f(x)的解析式及单调递增区间;
(Ⅱ)将f(x)的图象向右平移![]() 单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0,
单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0, ![]() ]上恒成立,求实数a的取值范围.
]上恒成立,求实数a的取值范围.
【答案】(Ⅰ)f(x)=sin(x+![]() ),
),![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(1)利用向量的坐标运算得到![]() ,再由f(
,再由f(![]() -x)=f(x)可知函数f(x)的图象关于直线x=
-x)=f(x)可知函数f(x)的图象关于直线x=![]() 对称,所以
对称,所以![]() +φ=
+φ=![]() +kπ,进而得到φ=
+kπ,进而得到φ=![]() ,利用三角函数的性质求解单调区间即可;
,利用三角函数的性质求解单调区间即可;
(2)将f(x)的图象向右平移![]() 单位得g(x)= sinx,即sinx+1≤ax+cosx在x∈[0,
单位得g(x)= sinx,即sinx+1≤ax+cosx在x∈[0,![]() ]上恒成立,利用数形结合分别研究h(x)=sinx-cosx和φ(x)= ax—1即可.
]上恒成立,利用数形结合分别研究h(x)=sinx-cosx和φ(x)= ax—1即可.
试题解析:
(Ⅰ)∵f(x)=![]()
![]() =sinxcosφ+cosxsinφ=sin(x+φ),
=sinxcosφ+cosxsinφ=sin(x+φ),
再由f(![]() -x)=f(x)可知函数f(x)的图象关于直线x=
-x)=f(x)可知函数f(x)的图象关于直线x=![]() 对称,
对称,
∴![]() +φ=
+φ=![]() +kπ,k∈Z,又|φ|<
+kπ,k∈Z,又|φ|<![]() ,∴φ=
,∴φ=![]()
∴f(x)=sin(x+![]() ),
),
由2kπ-![]() ≤ x+
≤ x+![]() ≤2kπ+
≤2kπ+![]() 可得2kπ-
可得2kπ-![]() ≤x≤ 2kπ+
≤x≤ 2kπ+![]() ,
,
∴函数的递增区间为[2kπ-![]() ,2kπ+
,2kπ+![]() ],k∈Z;
],k∈Z;
(Ⅱ)由图象平移易知g(x)=sinx,即sinx+1≤ax+cosx在x∈[0,![]() ]上恒成立.
]上恒成立.
也即sinx-cosx≤ax-1在x∈[0,![]() ]上恒成立.
]上恒成立.
令h(x)=sinx-cosx=![]() sin(x-
sin(x-![]() ),x∈[0,
),x∈[0,![]() ];
];
φ(x)= ax-1
如下图:h(x)的图象在φ(x)图象的下方,

则: a ≥kAB=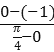 =
=![]() ,故
,故![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们知道:人们对声音有不同的感觉,这与它的强度有关系.声音的强度![]() 用瓦/米2 (
用瓦/米2 (![]() )表示,但在实际测量时,常用声音的强度水平
)表示,但在实际测量时,常用声音的强度水平![]() 表示,它们满足以下公式:
表示,它们满足以下公式: ![]() (单位为分贝,
(单位为分贝, ![]() ,其中
,其中![]() ,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:
,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:
(1)树叶沙沙声的强度是![]() ,耳语的强度是
,耳语的强度是![]() ,恬静的无线电广播的强度是
,恬静的无线电广播的强度是![]() ,试分别求出它们的强度水平;
,试分别求出它们的强度水平;
(2)某一新建的安静小区规定:小区内公共场所的声音的强度水平必须保持在50分贝以下,试求声音强度![]() 的范围为多少?
的范围为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
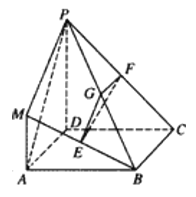
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(-2),f(3),f(-![]() )的大小顺序是:( )
)的大小顺序是:( )
A. f(-![]() )>f(3)>f(-2) B. f(-
)>f(3)>f(-2) B. f(-![]() ) >f(-2)>f(3)
) >f(-2)>f(3)
C. f(-2)>f(3)> f(-![]() ) D. f(3)>f(-2)> f(-
) D. f(3)>f(-2)> f(-![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com