
【题目】设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(-2),f(3),f(-![]() )的大小顺序是:( )
)的大小顺序是:( )
A. f(-![]() )>f(3)>f(-2) B. f(-
)>f(3)>f(-2) B. f(-![]() ) >f(-2)>f(3)
) >f(-2)>f(3)
C. f(-2)>f(3)> f(-![]() ) D. f(3)>f(-2)> f(-
) D. f(3)>f(-2)> f(-![]() )
)
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】某区工商局、消费者协会在![]() 月
月![]() 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取![]() 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
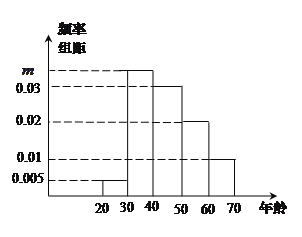
(Ⅰ)若电视台记者要从抽取的群众中选![]() 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第![]() 组或第
组或第![]() 组的概率;
组的概率;
(Ⅱ)已知第![]() 组群众中男性有
组群众中男性有![]() 人,组织方要从第
人,组织方要从第![]() 组中随机抽取
组中随机抽取![]() 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosφ,sinφ)(|φ|<
=(cosφ,sinφ)(|φ|<![]() ).函数
).函数
f(x)=![]()
![]() 且f(
且f(![]() -x)=f(x).
-x)=f(x).
(Ⅰ)求f(x)的解析式及单调递增区间;
(Ⅱ)将f(x)的图象向右平移![]() 单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0,
单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0, ![]() ]上恒成立,求实数a的取值范围.
]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以平面直角坐标系的原点
为参数).以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 和
和![]() 公共弦的长度.
公共弦的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com