【题目】同时掷两个骰子，计算：
（1）一共有多少种不同的结果？
（2）其中向上的点数之和是5的结果有多少种？
（3）向上的点数之和是5的概率是多少？
【答案】（1）如解析所示；（2）
【解析】【试题分析】（1）先将同时投掷两个骰子的点数全部列举出来；（2）列举出来点数之和是5的所有可能结果（1，4），（2，3）（3，2）（4，1），共四种；（3）依据题设中要求“向上的点数之和是5”，运用古典概型的计算公式求出满足题设条件的事件的概率为
。
解：（1）
1点 | 2点 | 3点 | 4点 | 5点 | 6点 | |
1点 | （1,1） | （1,2） | （1,3） | （1,4） | （1,5） | （1,6） |
2点 | （2,1） | （2,2） | （2,3） | （2,4） | （2,5） | （2,6） |
3点 | （3,1） | （3,2） | （3,3） | （3,4） | （3,5） | （3,6） |
4点 | （4,1） | （4,2） | （4,3） | （4,4） | （4,5） | （4,6） |
5点 | （5,1） | （5,2） | （5,3） | （5,4） | （5,5） | （5,6） |
6点 | （6,1） | （6,2） | （6,3） | （6,4） | （6,5） | （6,6） |
掷一个骰子的结果有6种。我们把两个标上记号1、2以便区分，由于1号骰子 的每一个结果都可与2号骰子的任意一个结果配对，组成同时掷两个骰子的一个结果，因此同时掷两个骰子的结果共有36种。
（2）在上面的所有结果中，向上的点数之和为5的结果有（1，4），（2，3）（3，2）（4，1）
其中第一个数表示1号骰子的结果，第二个数表示2号骰子的结果。
由于所有36种结果是等可能的，其中向上点数之和为5的结果（记为事件A）有4种，因此，由古典概型的概率计算公式可得 
科目：高中数学 来源： 题型：
【题目】某省两相近重要城市之间人员交流频繁，为了缓解交通压力，特修一条专用铁路，用一列火车作为交通车，已知该车每次拖4节车厢，一日能来回16次，如果每次拖7节车厢，则每日能来回10次．
（1）若每日来回的次数是车头每次拖挂车厢节数的一次函数，求此一次函数解析式：
（2）在（1）的条件下，每节车厢能载乘客110人．问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，四边形
是正方形， 
平面
， 
分别为
的中点，且
.
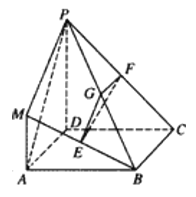
（1）求证：平面
平面
；
（2）求证：平面
平面
；
（3）求三棱锥
与四棱锥
的体积之比.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f(x)是R上的偶函数，且在[0,+∞)上单调递增，则f(-2),f(3),f(-
)的大小顺序是：（ ）
A. f(-
)>f(3)>f(-2) B. f(-
) >f(-2)>f(3)
C. f(-2)>f(3)> f(-
) D. f(3)>f(-2)> f(-
)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x3+ax2+bx+a2.
（I）若f（x）在x=1处有极值10，求a，b的值；
（II）若当a=-1时，f（x）<0在x∈[1，2]恒成立，求b的取值范围
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】袋中装有偶数个球，其中红球、黑球各占一半，甲、乙、丙是三个空盒.每次从袋中任取两个球，将其中一个球放入甲盒，如果这个球是红球，就将另一个球放入乙盒，否则就放入丙盒.重复上述过程，直到袋中所有球都放入盒中，则（ ）
A. 乙盒中红球与丙盒中黑球一样多
B. 乙盒中黑球不多于丙盒中黑球
C. 乙盒中红球不多于丙盒中红球
D. 乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，直线
与反比例函数
的图象交于B、C两点，B（2，m）且m＜2，正方形ABCD的顶点A、D在坐标轴上。
⑴ 求
， 
的值；
⑵ 直接写出
时， 
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
