
分析 (1)设直线l:y+1=k(x-1).求得N的坐标,联立直线方程和双曲线方程,运用韦达定理和判别式,计算即可得到k的范围;
(2)由向量的共线的坐标表示,可得λ1、λ2是方程(t2-4)λ2+(2t-8)λ-7=0的两个根,运用韦达定理,结合二次函数的值域求法,化简计算即可得到所求范围.
解答 解:(1)设直线l:y+1=k(x-1).则N$(\frac{1}{k}+1,0)$.设A(x1,y1),B(x2,y2).
将直线l的方程代入双曲线C的方程得(1-4k2)x2+8k(k+1)x-4((k+1)2-4=0.①
因为方程①有两个不同的正根x1,x2,所以△=64k2(k+1)2=16(1-4k2)[1+(k+1)2]>0,
且x1+x2=$\frac{8k(k+1)}{4{k}^{2}-1}$>0,x1x2=$\frac{4+4(k+1)^{2}}{4{k}^{2}-1}$>0,
解得$\frac{1}{2}$<k<$\frac{1+\sqrt{7}}{3}$;
(2)由$\overrightarrow{MA}={λ_1}\overrightarrow{AN}$,可得x1=$\frac{1+{λ}_{1}(\frac{1}{k}+1)}{1+{λ}_{1}}$,y1=$\frac{-1}{1+{λ}_{1}}$,将其代入双曲线方程可得,
[($\frac{1}{k}$+1)2-4]λ12+2[2($\frac{1}{k}$+1)-8]λ1-7=0,
同理可得[($\frac{1}{k}$+1)2-4]λ22+2[2($\frac{1}{k}$+1)-8]λ2-7=0,
于是λ1、λ2是方程(t2-4)λ2+(2t-8)λ-7=0的两个根,其中t=$\frac{1}{k}$+1∈($\frac{\sqrt{7}+1}{2}$,3),
则λ1+λ2=$\frac{2t-8}{4-{t}^{2}}$,λ1λ2=$\frac{7}{4-{t}^{2}}$,
故$\frac{λ_1}{λ_2}+\frac{λ_2}{λ_1}$=$\frac{({λ}_{1}+{λ}_{2})^{2}}{{λ}_{1}{λ}_{2}}$-2=$\frac{(2t-8)^{2}}{7(4-{t}^{2})}$-2,
令z=t-4∈($\frac{\sqrt{7}-7}{2}$,-1),
则$\frac{λ_1}{λ_2}+\frac{λ_2}{λ_1}$=-$\frac{4}{7(\frac{12}{{z}^{2}}+\frac{8}{z}+1)}$-2,
由$\frac{12}{{z}^{2}}$+$\frac{8}{z}$+1=12($\frac{1}{z}$+$\frac{1}{3}$)2-$\frac{1}{3}$∈(-$\frac{1}{7}$,5),
则有$\frac{λ_1}{λ_2}+\frac{λ_2}{λ_1}$∈(-∞,-$\frac{74}{35}$)∪(2,+∞).
点评 本题考查双曲线的方程和性质,考查直线和双曲线方程联立,运用韦达定理,同时考查向量的坐标表示,二次函数的值域的求法,考查运算能力,属于中档题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{5}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{6}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
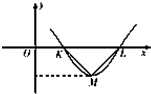 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )| A. | $-\frac{{\sqrt{3}}}{4}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com