
���� ��1���Ķ��ó��ӻ�õ�һ�������ʤ�Ҷ��Ҽ�ʤ���ӣ��ӻ�õ�һ���ĸ���Ϊ${P_1}��{P_2}=\frac{1}{6}$�� �Ҷӻ�õ�һ���ĸ���Ϊ$��1-{P_1}����\frac{1}{5}=\frac{1}{15}$����ⷽ���鼴�ɣ�
��2����������ó�X����ȡ��ֵΪ��0��3��6���ֱ�������ʵó��ֲ��м��ɣ������ѧ������
��� �⣺���������⣬�ӻ�õ�һ�������ʤ�Ҷ��Ҽ�ʤ���ӣ�
��ӻ�õ�һ���ĸ���Ϊ${P_1}��{P_2}=\frac{1}{6}$�� ��
ͬ�����Ҷӻ�õ�һ���ĸ���Ϊ$��1-{P_1}����\frac{1}{5}=\frac{1}{15}$����
�ɢ٢ڵã�${P_1}=\frac{2}{3}��{P_2}=\frac{1}{4}$��
���Լ�սʤ�Ҷӵĸ���Ϊ$\frac{2}{3}$����սʤ���ӵĸ���$\frac{1}{4}$��
����$P��X=0��=��1-\frac{2}{3}����1-\frac{1}{4}��=\frac{1}{4}$��
$P��X=3��=\frac{2}{3}��1-\frac{1}{4}��+��1-\frac{2}{3}��\frac{1}{4}=\frac{7}{12}$��
$P��X=6��=\frac{2}{3}��\frac{1}{4}=\frac{1}{6}$��
X�ķֲ���Ϊ��
| X | 0 | 3 | 6 |
| P | $\frac{1}{4}$ | $\frac{7}{12}$ | $\frac{1}{6}$ |
���� ���⿼���˹ŵ������ʵ�������е�Ӧ�ã�������ѧ�����Ķ��������������������������е��⣮


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
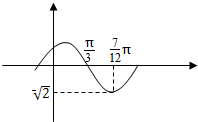 ����f��x��=Asin����x+�գ���A��0���أ�0��-$\frac{��}{2}$���գ�$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ��
����f��x��=Asin����x+�գ���A��0���أ�0��-$\frac{��}{2}$���գ�$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��4] | B�� | [0��$\frac{4}{3}$] | C�� | [0��$\frac{1}{2}$] | D�� | ��-�ޣ�0]�ȣ�$\frac{4}{3}$��+��] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | e | B�� | 2e | C�� | 3e | D�� | 4e |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com