Question

19．设集合A={（x，y）|（x-4）²+y²=1}，B={（x，y）|（x-t）²+（y-at+2）²=1}，如果命题“?t∈R，A∩B≠∅”是真命题，则实数a的取值范围是（　　）

• A． [1，4]
• B． [0，$\frac{4}{3}$]
• C． [0，$\frac{1}{2}$]
• D． （-∞，0]∪（$\frac{4}{3}$，+∞]

Answer 1

分析 首先要将条件进行转化，即命题P：A∩B≠∅为假命题，再结合集合A、B的特征利用数形结合即可获得必要的条件，解不等式组即可获得问题的解答．

解答 解：∵A={（x，y）|（x-4）²+y²=1}，表示平面坐标系中以M（4，0）为圆心，半径为1的圆，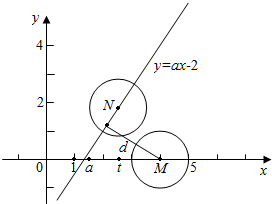

B={（x，y）|（x-t）²+（y-at+2）²=1}，表示以N（t，at-2）为圆心，半径为1的圆，且其圆心N在直线ax-y-2=0上，如图．
如果命题“?t∈R，A∩B≠∅”是真命题，即两圆有公共点，则圆心M到直线ax-y-2=0的距离不大于2，
即 $\frac{|4a-2|}{\sqrt{{a}^{2}+1}}$≤2，解得0≤a≤$\frac{4}{3}$．
∴实数a的取值范围是[0，$\frac{4}{3}$]；
故选：B．

点评 本题考查的是集合运算和命题的真假判断与应用的综合类问题．在解答的过程当中充分体现了圆的知识、集合运算的知识以及命题的知识．同时问题转化的思想也在此题中得到了很好的体现．值得同学们体会和反思．