
【题目】已知抛物线![]()
![]() ,过焦点
,过焦点![]() 的斜率存在的直线与抛物线交于
的斜率存在的直线与抛物线交于![]() ,
,![]() ,且
,且![]() .
.
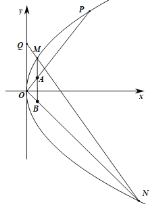
(1)求抛物线的方程;
(2)已知![]() 与抛物线交于点
与抛物线交于点![]() (异于原点),过点
(异于原点),过点![]() 作斜率小于
作斜率小于![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() ,
,![]() 之间),过点
之间),过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于
于![]() ,交
,交![]() 于B,
于B,![]() 与
与![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
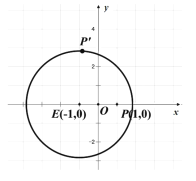
【题目】如图,一张坐标纸上一已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于两个不同的点
交于两个不同的点![]() ,且直线
,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 为动点,以
为动点,以![]() 为直径的圆内切于
为直径的圆内切于![]() .
.
(1)证明![]() 为定值,并求点
为定值,并求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,直线
两点,直线![]() 过点
过点![]() 且与
且与![]() 垂直,
垂直,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 为
为![]() 的中点,求
的中点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
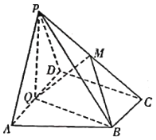
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
(1)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 面
面![]() ;
;
(2)若二面角![]() 为
为![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() ,
,![]() ,(其中
,(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 、
、![]() 如图所示.
如图所示.

(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com