
设函数f(x)= a为常数且a∈(0,1).
a为常数且a∈(0,1).
(1)当a= 时,求f
时,求f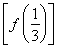 ;
;
(2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f[f(x1)]),B(x2,f[f(x2)]),C(a2,0),记△ABC的面积为S(a),求S(a)在区间[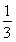 ,
, ]上的最大值和最小值.
]上的最大值和最小值.
(1)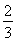 (2)见解析,x1=
(2)见解析,x1= ,x2=
,x2= (3)最小值为
(3)最小值为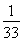 ,最大值为
,最大值为
【解析】(1)当a= 时,f
时,f =
= ,f
,f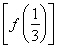 =f
=f =2
=2 =
=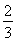 .
.
(2)证明:f[f(x)]=
当0≤x≤a2时,由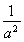 x=x解得x=0,由于f(0)=0,故x=0不是f(x)的二阶周期点;
x=x解得x=0,由于f(0)=0,故x=0不是f(x)的二阶周期点;
当a2<x≤a时,由 (a-x)=x解得x=
(a-x)=x解得x= ∈(a2,a),因为f
∈(a2,a),因为f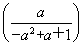 =
=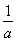 ·
· =
=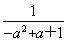 ≠
≠ ,故x=
,故x= 是f(x)的二阶周期点;
是f(x)的二阶周期点;
当a<x<a2-a+1时,由 (x-a)=x解得x=
(x-a)=x解得x=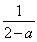 ∈(a,a2-a+1),
∈(a,a2-a+1),
因为f =
=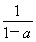 ·
·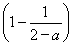 =
=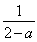 ,故x=
,故x= 不是f(x)的二阶周期点;
不是f(x)的二阶周期点;
当a2-a+1≤x≤1时,由 (1-x)=x解得x=
(1-x)=x解得x=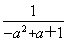 ∈(a2-a+1,1),因为f
∈(a2-a+1,1),因为f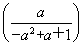 =
=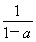 ·
·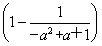 =
= ≠
≠ ,故x=
,故x= 是f(x)的二阶周期点.
是f(x)的二阶周期点.
因此,函数f(x)有且仅有两个二阶周期点,x1= ,x2=
,x2= .
.
(3)由(2)得A( ,
, ),B(
),B( ,
, ),则S(a)=
),则S(a)=
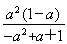 ,
,
S′(a)= ·
·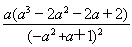 .
.
因为a∈[ ,
, ],有a2+a<1,所以S′(a)=
],有a2+a<1,所以S′(a)= ·
·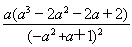 =
= ·
· >0.(或令g(a)=a3-2a2-2a+2,g′(a)=3a2-4a-2=3(a-
>0.(或令g(a)=a3-2a2-2a+2,g′(a)=3a2-4a-2=3(a- )(a-
)(a-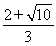 ),
),
因为a∈(0,1),所以g′(a)<0,则g(a)在区间[ ,
, ]上最小值为g(
]上最小值为g( )=
)=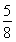 >0,故对于任意a∈[
>0,故对于任意a∈[ ,
, ],g(a)=a3-2a2-2a+2>0,S′(a)=
],g(a)=a3-2a2-2a+2>0,S′(a)= ·
·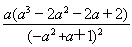 >0)则S(a)在区间[
>0)则S(a)在区间[ ,
, ]上单调递增,故S(a)在区间[
]上单调递增,故S(a)在区间[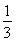 ,
, ]上的最小值为S(
]上的最小值为S( )=
)=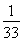 ,最大值为S(
,最大值为S( )=
)= .
.


科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集9讲练习卷(解析版) 题型:选择题
已知等比数列{an}中,各项均为正数,前n项和为Sn,且4a3,a5,2a4成等差数列,若a1=1,则S4=( )
A.7 B.8 C.15 D.16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集6讲练习卷(解析版) 题型:解答题
已知函数f(x)=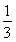 x3+ax2+bx(a,b∈R).
x3+ax2+bx(a,b∈R).
(1)当a=1时,求函数f(x)的单调区间;
(2)若f(1)=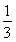 ,且函数f(x)在
,且函数f(x)在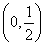 上不存在极值点,求a的取值范围.
上不存在极值点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集5讲练习卷(解析版) 题型:填空题
某工厂产生的废气经过过滤后排放,过滤前的废气的污染指数量为P0 mg/L,过滤过程中废气的污染指数量P mg/L与时间t h间的关系为P=P0e-kt.如果在前5个小时消除了10%的污染物,则10小时后还剩________%的污染物.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集5讲练习卷(解析版) 题型:选择题
函数f(x)=|x-2|-ln x在定义域内的零点个数为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集4讲练习卷(解析版) 题型:选择题
已知函数f(x)=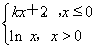 (k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
(k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
A.k≤2 B.-1<k<0 C.-2≤k<-1 D.k≤-2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集4讲练习卷(解析版) 题型:选择题
已知幂函数f(x)的图像经过点(9,3),则f(2)-f(1)=( )
A.3 B.1- C.
C.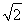 -1 D.1
-1 D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集3B讲练习卷(解析版) 题型:选择题
已知集合A={x∈R|2x+1<0},B={x∈R|(x+1)(x-2)<0},则A∩B=( )
A.(-∞,-1) B.  C.
C. D.(2,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集1B讲练习卷(解析版) 题型:填空题
若命题“存在实数x0,使x+ax0+1<0”的否定是真命题,则实数a的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com