
已知函数f(x)=2sin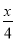 cos
cos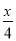 +
+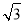 cos
cos .
.
(1)求函数f(x)的最小正周期及最值;
(2)令g(x)=f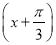 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
(1) 最小正周期4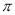 ;(2) 函数g(x)是偶函数.
;(2) 函数g(x)是偶函数.
【解析】
试题分析:(1)利用两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后直接求f(x)的最小正周期;(2)求出g(x)=f 的表达式,通过函数的奇偶性的定义,直接证明即可.
的表达式,通过函数的奇偶性的定义,直接证明即可.
试题解析: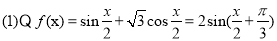 2分
2分
∴f(x)的最小正周期T=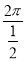 =4
=4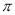 .1分
.1分
当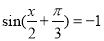 时,f(x)取得最小值-2; 1分
时,f(x)取得最小值-2; 1分
当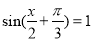 时,f(x)取得最大值2 .1分
时,f(x)取得最大值2 .1分
(2)g(x)是偶函数.理由如下: .1分
由(1)知 ,又g(x)
,又g(x)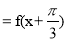
∴g(x)= 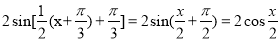 3..分
3..分
∵g(-x)= =g(x), .2分
=g(x), .2分
∴函数g(x)是偶函数 ..1分
考点:三角函数中的恒等变换应用;三角函数的周期性及其求法;正弦函数的奇偶性.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源:2016届辽宁省分校高一下学期期末考试数试卷(解析版) 题型:选择题
某初级中学领导采用系统抽样方法,从该校800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号,求得间隔数 ,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )
,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )
A.39 B.40 C.37 D.38
查看答案和解析>>
科目:高中数学 来源:2016届辽宁东北育才学校等三校高一下学期期末联考数学试卷(解析版) 题型:选择题
某时段内共有100辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为( )
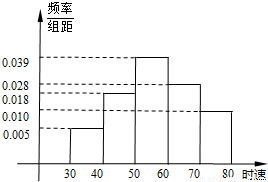
A.38辆 B.28辆 C.10辆 D.5辆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com