
 (文科)如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.
(文科)如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.| OB |
| cos∠OBC |
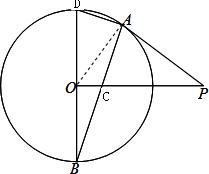 证明:(I)∵PA与圆O相切于点A,
证明:(I)∵PA与圆O相切于点A,| OA |
| OP |
| 3 |
| 5 |
| ∠AOP |
| 2 |
2
| ||
| 5 |
| ∠AOP |
| 2 |
| ||
| 5 |
| π |
| 2 |
π-(
| ||
| 2 |
| π |
| 4 |
| ∠AOP |
| 2 |
3
| ||
| 10 |
| OB |
| cos∠OBC |
| 3 | ||||
|
| 10 |


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
 (2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.
(2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).| p2 |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
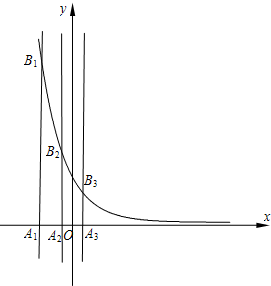 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:浙江省海盐元济高级中学2010-2011学年高二12月月考数学试题 题型:044
如图,已知正三角形PAB⊥底面ABCD,其中∠ABC=∠BAD=90°且BC=2AD=2AB=4,
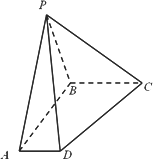
(Ⅰ)求证:AD∥平面PBC
(Ⅱ)求四棱锥P-ABCD的体积
(Ⅲ)求PC与底面ABCD所成角的余弦值(文科)
求二面角P-CD-B的余弦值(理科)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
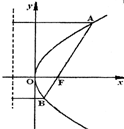 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2). ;
; 时,求弦长|AB|.
时,求弦长|AB|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com