
 的极小值点,
的极小值点,解:易知f′n(x)=x2-(3an+n2)x+3n2an=(x-3an)(x-n2),
令f′n(x)=0,得x1=3an,x2=n2,
①若3an<n2,则当x<3an时,f′n(x)>0,fn(x)单调递增;
当3an<x<n2时, f′n(x)<0,fn(x)单调递减;
当x>n2时,f′n(x)>0,fn(x)单调递增;
故fn(x)在x=n2取得极小值.
②若3an>n2,仿①可得,fn(x)在x=3an取得极小值;
③若3an=n2,则f′n(x)≥0,fn(x)无极值。
(Ⅰ)当a=0时,a1=0,则3a1<12,由(1)知,a2=12=1,
因3a2=3<22,则由(1)知,a3=22=4,
因为3a3=12>32,则由(2)知,a4=3a3=3×4.
又因为3a4=36>42,则由(2)知,a5=3a4=32×4.
由此猜测:当n≥3时,an=4×3n-3,
下面先用数学归纳法证明,当n≥3时,3an>n2.
事实上,当n=3时,由前面的讨论知结论成立.
假设当n=k(k≥3)时,3ak>k2成立,
则由(2)知,ak+1=3ak>k2,
从而3ak+1-(k+1)2>3k2-(k+1)2=2k(k-2)+2k-1>0,
所以3ak+1>(k+1)2,
故当n≥3时,3an>n2成立;
于是由(2)知,当n≥3时,an+1=3an,而a3=4,因此an=4×3n-3;
综上所述,当a=0时,a1=0,a2=1,an=4×3n-3(n≥3)。
(Ⅱ)存在a,使数列{an}是等比数列.
事实上,由(2)知,若对任意的n,都有3an>n2,则an+1=3an,
即数列{an}是首项为a,公比为3的等比数列,且an=a·3n-1,
而要使3an≥n2,即a·3n>n2对一切n∈N*都成立,只需a>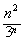 对一切n∈N*都成立,
对一切n∈N*都成立,
记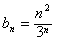 ,则
,则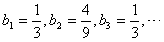 ,
,
令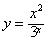 ,则
,则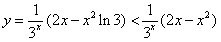 ,
,
因此,当x≥2时,y′<0,从而函数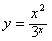 在[2,+∞)上单调递减;
在[2,+∞)上单调递减;
故当n≥2时,数列{bn}单调递减,即数列{bn}中最大项为b2=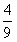 ,
,
于是当a>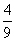 时,必有
时,必有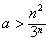 ,这说明,当a∈
,这说明,当a∈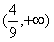 时,数列{an}是等比数列;
时,数列{an}是等比数列;
当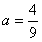 时,可得
时,可得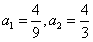 ,
,
而3a2=4=22,由(3)知,f2(x)无极值,不合题意;
当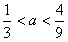 时,可得a1=a,a2=3a,a3=4,a4=12,…,数列{an}不是等比数列;
时,可得a1=a,a2=3a,a3=4,a4=12,…,数列{an}不是等比数列;
当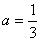 时,3a=1=12,由(3)知,f1(x)无极值,不合题意;
时,3a=1=12,由(3)知,f1(x)无极值,不合题意;
当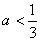 时,可得a1=a,a2=1,a3=4,a4=12,…,数列{an}不是等比数列;
时,可得a1=a,a2=1,a3=4,a4=12,…,数列{an}不是等比数列;
综上所述,存在a,使数列{an}是等比数列,且a的取值范围为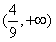 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 5 |
| 2 |
| an+bn |
| 2 |
| 2anbn |
| an+bn |
| an+2 |
| an-2 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n-1 |
| 2n |
| 1 |
| bn-n |
| 37 |
| 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com