
 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于 ,线段
,线段 为圆
为圆 的弦,
的弦, 垂直于圆
垂直于圆 所在平面,垂足
所在平面,垂足 是圆
是圆 上异于
上异于 、
、 的点,
的点, ,圆
,圆 的直径为9。
的直径为9。
 平面
平面 ;
; 的平面角的正切值。
的平面角的正切值。 的平面角的正切值为
的平面角的正切值为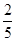 。
。 垂直于圆
垂直于圆 所在平面,
所在平面, 在圆
在圆 所在平面上,
所在平面上,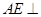
 。
。 中,
中,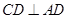 ,
,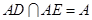 ,∴
,∴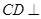 平面
平面 .∵
.∵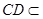 平面
平面 ,
, 平面
平面 。 ……………………………………………6分
。 ……………………………………………6分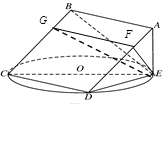
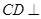 平面
平面 ,
,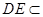 平面
平面 ,
, 。
。 为圆
为圆 的直径,即
的直径,即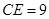 .
. 的边长为
的边长为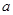 ,
,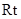 △
△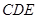 中,
中,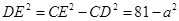 ,
,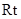 △
△ 中,
中,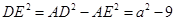 ,
,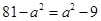 ,解得,
,解得,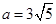 。 ∴
。 ∴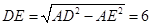 。
。 作
作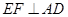 于点
于点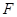 ,作
,作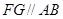 交
交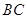 于点
于点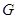 ,连结
,连结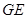 ,
,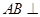 平面
平面 ,
,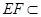 平面
平面 ,∴
,∴ 。∵
。∵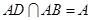 ,
, 平面
平面 。∵
。∵ 平面
平面 ,
,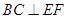 。∵
。∵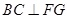 ,
,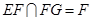 ,
,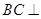 平面
平面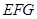 。∵
。∵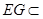 平面
平面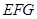 ,∴
,∴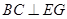 。
。 是二面角
是二面角 的平面角。…………………………………10分
的平面角。…………………………………10分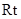 △
△ 中,
中,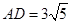 ,
, ,
,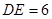 ,
,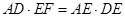 ,∴
,∴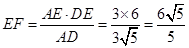 。
。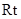 △
△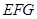 中,
中,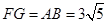 ,∴
,∴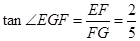 。
。 的平面角的正切值为
的平面角的正切值为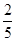 。 …………………………12分
。 …………………………12分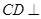 平面
平面 ,
,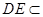 平面
平面 ,
, 。∴
。∴ 为圆
为圆 的直径,即
的直径,即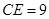 。
。  的边长为
的边长为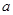 ,在
,在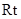 △
△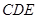 中,
中,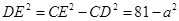 ,
,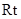 △
△ 中,
中,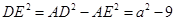 ,
,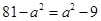 ,解得,
,解得,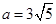 。∴
。∴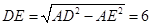 。
。 为坐标原点,分别以
为坐标原点,分别以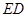 、
、 所在的直线为
所在的直线为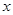 轴、
轴、 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
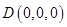 ,
,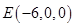 ,
,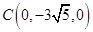 ,
,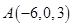 ,
, 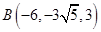 。……………8分
。……………8分 的法向量为
的法向量为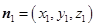 ,
, 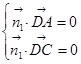 即
即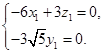
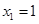 ,则
,则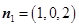 是平面
是平面 的一个法向量。…………9分
的一个法向量。…………9分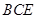 的法向量为
的法向量为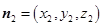 ,则
,则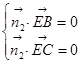 即
即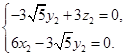
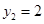 ,则
,则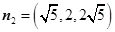 是平面
是平面 的一个法向量。…………10分
的一个法向量。…………10分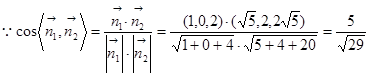 ,
,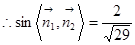 .
.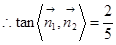
 的平面角的正切值为
的平面角的正切值为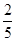


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源:不详 题型:单选题
| A.内心 | B.重心 | C.外心 | D.垂心 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
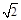 .将
.将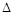 ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,| A.存在某个位置,使得直线AC与直线BD垂直 |
| B.存在某个位置,使得直线AB与直线CD垂直 |
| C.存在某个位置,使得直线AD与直线BC垂直 |
| D.对任意位置,三直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com