
分析 (1)根据偶函数的定义可得k的值;
(2)构造函数h(x)=f(x)-g(x),根据对数函数的图象和性质可得,只需要t>-2x+$\sqrt{x}$+2恒成立,根据二次函数的性质求出t的取值范围即可;
(3)先判断函数y=|f(x)|的单调性,令|2loga(2x+2)|=2,得到x=$\frac{a-2}{2}$或$\frac{1-2a}{2a}$,即可得到n-m的最小值为(-$\frac{1}{2}$)-$\frac{a-2}{2}$=$\frac{1}{6}$,求出a即可.
解答 解:(1)∵函数y=g(ax+1)-kx是偶函数,
∴loga(a-x+1)+kx=loga(ax+1)-kx,对任意x∈R恒成立,
∴2kx=loga(ax+1)-loga(a-x+1)=loga($\frac{{a}^{x}+1}{{a}^{-x}+1}$)=x
∴k=$\frac{1}{2}$,
(2)由题意设h(x)=f(x)-g(x)=2loga(2x+t-2)-logax<0在x∈[1,4]恒成立,
∴2loga(2x+t-2)<logax,
∵0<a<1,x∈[1,4],
∴只需要2x+t-2>$\sqrt{x}$恒成立,
即t>-2x+$\sqrt{x}$+2恒成立,
∴t>(-2x+$\sqrt{x}$+2)max,
令y=-2x+$\sqrt{x}$+2=-2($\sqrt{x}$)2+$\sqrt{x}$+2=-2($\sqrt{x}$-$\frac{1}{4}$)2+$\frac{17}{8}$,x∈[1,4],
∴(-2x+$\sqrt{x}$+2)max=1,
∴t的取值范围是t>1,
(3)∵t=4,0<a<1,
∴函数y=|f(x)|=|2loga(2x+2)|在(-1,-$\frac{1}{2}$)上单调递减,在(-$\frac{1}{2}$,+∞)上单调递增,
∵当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],且f(-$\frac{1}{2}$)=0,
∴-1<m≤$-\frac{1}{2}$≤n(等号不同时取到),
令|2loga(2x+2)|=2,得x=$\frac{a-2}{2}$或$\frac{1-2a}{2a}$,
又[$\frac{1-2a}{2a}$-(-$\frac{1}{2}$)]-[(-$\frac{1}{2}$)-$\frac{a-2}{2}$]=$\frac{(a-1)^{2}}{2a}$>0,
∴$\frac{1-2a}{2a}$-(-$\frac{1}{2}$)>(-$\frac{1}{2}$)-$\frac{a-2}{2}$,
∴n-m的最小值为(-$\frac{1}{2}$)-$\frac{a-2}{2}$=$\frac{1}{6}$,
∴a=$\frac{2}{3}$.
点评 本题考查了对数函数的性质以及偶函数的性质和函数恒成立问题,以及函数的最值问题,考查了学生的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [-2,1] | C. | [-2,-1] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
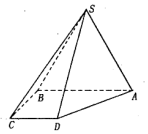 如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.
如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com