
【题目】命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点;命题q:曲线![]() ﹣
﹣![]() =1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
=1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
【答案】解:∵命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点,
∴圆心到直线的距离d=![]() ,∴k
,∴k![]() 2
2![]() 或k
或k![]() -2
-2![]() ,
,
∵命题q:曲线![]() ﹣
﹣![]() =1表示焦在y轴上的双曲线,
=1表示焦在y轴上的双曲线,
∴![]() ,解得k<0,
,解得k<0,
∵p∧q为真命题,∴p,q均为真命题,
∴![]() ,
,
解得k<﹣2![]() .
.
【解析】命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点,可得圆心到直线的距离d=![]() , 解得k范围.命题q:曲线
, 解得k范围.命题q:曲线![]() ﹣
﹣![]() =1表示焦在y轴上的双曲线,可得
=1表示焦在y轴上的双曲线,可得![]() , 解得k范围.由于p∧q为真命题,可得p,q均为真命题,即可得出.
, 解得k范围.由于p∧q为真命题,可得p,q均为真命题,即可得出.
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度υ(千米/小时)之间的函数关系为:y= ![]() (υ>0).
(υ>0).
(1)在该时段内,当汽车的平均速度υ为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的首项为1,公比为q,它的前n项和为Sn;
(1)若S3=3,S6=﹣21,求公比q;
(2)若q>0,且Tn=a1+a3+…+a2n﹣1 , 求 ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列
(1)在等差数列{an}中,a6=10,S5=5,求该数列的第8项a8;
(2)在等比数列{bn}中,b1+b3=10,b4+b6= ![]() ,求该数列的前5项和S5 .
,求该数列的前5项和S5 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,圆C的方程为x2+y2﹣8x+15=0,若直线y=kx+2上至少存在一点,使得以该点为圆心,半径为1的圆与圆C有公共点,则k的最小值是( )
A.-![]()
B.-![]()
C.-![]()
D.-![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南通一模19】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若![]() ,证明:函数
,证明:函数![]() 有且只有一个零点;
有且只有一个零点;
(3)若函数![]() 又两个零点,求实数
又两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【南通市、泰州市2017届高三第一次调研测试】(本题满分14分)如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,焦点到相应准线的距离为1.
,焦点到相应准线的距离为1.
(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线
![]() 于点Q,求
于点Q,求![]() 的值;
的值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是棱AB上的动点.
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45°,求![]() 的值.
的值.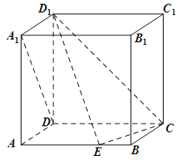
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com