
3.
(1)解:由奇函数的对称性可知,我们只要讨论f(x)在区间(-∞,0)的单调性即可.
f ′(x)=2+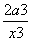 ,令f ′(x)=0,得x=-a.
,令f ′(x)=0,得x=-a.
①当a≤0时,f ′(x)>0,故f(x)在区间(-∞,0)是单调递增. …
②当a>0时,x ∈(-∞,-a ),f ′(x)>0,所以f(x)在区间(-∞,-a )是单调递增.
x ∈(-a,0),f ′(x)<0,所以f(x)在区间(-a,0)是单调减.
综上所述:当a≤0时,f(x)单调增区间为(-∞,0),(0,+∞);当a>0时,f(x)单调增区间为(-∞,-a ),(a ,+∞),单调减区间为(-a,0),(0,a).
(2)解:因为f(x)为奇函数,
所以当x>0时,f(x)=-f(-x)=-(-2 x-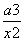 +1)=2x+
+1)=2x+ 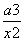 -1.
-1.
①当a<0时,要使f(x)≥a-1对一切x>0成立,即2x+ 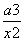 ≥a对一切x>0成立.
≥a对一切x>0成立.
而当x=-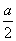 >0时,有-a+4a≥a,所以a≥0,则与a<0矛盾.
>0时,有-a+4a≥a,所以a≥0,则与a<0矛盾.
所以a<0不成立.
②当a=0时,f(x)=2x-1>-1=a-1对一切x>0成立,故a=0满足题设要求.
③当a>0时,由(1)可知f(x)在(0,a)是减函数,在(a ,+∞)是增函数.
所以 fmin(x)=
fmin(x)= f(a)=3a-1>a-1,所以a>0时也满足题设要求.
f(a)=3a-1>a-1,所以a>0时也满足题设要求.
综上所述,a的取值范围是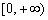 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数f(x)=ex-ax-1(a∈R).
(1)讨论f(x)=ex-ax-1(a∈R)的单调性;
(2)若a=1,求证:当x≥0时,f(x)≥f(-x).
查看答案和解析>>
科目:高中数学 来源: 题型:
抽样统计甲,乙两个城市连续5天的空气质量指数(AQI),数据如下:
| 城市[来源:Zxxk.Com][来源:学科网][来源:Z+xx+k.Com][来源:Z.xx.k.Com] | 空气质量指数(AQI) | ||||
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | |
| 甲 | 109 | 111 | 132 | 118 | 110 |
| 乙 | 110 | 111 | 115 | 132 | 112 |
则空气质量指数(AQI)较为稳定(方差较小)的城市为 (填甲或乙).
查看答案和解析>>
科目:高中数学 来源: 题型:
下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是
A.30.5 B.31.5 C.31 D.32
| 1 | 0 | 2 | ||
| 2 | 0 | 1 | 4 | |
| 3 | 1 | 1 | 2 | 6 |
| 4 | 3 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com