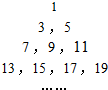Question

6．将正奇数排成如图所示的三角形数表：
其中第i行第j个数记为a_ij（i、j∈N^*），例如a₄₂=15，若a_ij=2015，则i+j=63．

Answer 1

分析 分析正奇数排列的正三角图表知，第i行（其中i∈N*）有i个奇数，且从左到右按从小到大的顺序排列，则2015是第1008个奇数，由等差数列的知识可得，它排在第几行第几个数

解答 解：根据正奇数排列的正三角图表知，2015是第1008个奇数，应排在i行（其中i∈N*），
则1+2+3+…+（i-1）=$\frac{1}{2}$ i（i-1）＜1008①，
且1+2+3+…+i=$\frac{1}{2}$ i（i+1）＞1006②；
验证i=45时，①②式成立，所以i=45；
第45行第1个奇数是2×$\frac{1}{2}$×44×45+1=1981，
而1981+2（j-1）=2015，
∴j=18；
所以，2015在第45行第18个数，则i+j=63．
故答案为：63

点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．