
【题目】集合![]() 、
、![]() 为
为![]() 的一个等浓二分划(即
的一个等浓二分划(即![]() ,
,![]() ,且
,且![]() .记集合
.记集合![]() 中所有数的积为
中所有数的积为![]() ,集合
,集合![]() 中所有数的积为
中所有数的积为![]() ,称
,称![]() 为
为![]() 的等浓二分划的特征数.证明:
的等浓二分划的特征数.证明:
(1)集合![]() 的等浓二分划的特征数一定为合数;
的等浓二分划的特征数一定为合数;
(2)若等浓二分划的特征数不为2的倍数,则该特征数为![]() 的倍数.
的倍数.
注:有限集合![]() 的元素个数简记为
的元素个数简记为![]() .
.
【答案】(1)见解析;(2)![]()
【解析】
(1)集合![]() 中的2014个数恰有1007个偶数,1007个奇数.
中的2014个数恰有1007个偶数,1007个奇数.
若全部偶数不全在![]() 、
、![]() 的同一个集合中,则
的同一个集合中,则![]() 、
、![]() 每个集合中均含偶数.
每个集合中均含偶数.
于是,![]() 与
与![]() 被2整除.
被2整除.
因此,![]() 被2整除.
被2整除.
若全部偶数均在![]() 、
、![]() 的一个集合中,不妨设集合
的一个集合中,不妨设集合![]() 的1007个元素全为偶数,则集合
的1007个元素全为偶数,则集合![]() 的1007个元素全为奇数.
的1007个元素全为奇数.
显然,集合![]() 中包含偶数6,集合
中包含偶数6,集合![]() 中包含奇数3.
中包含奇数3.
于是,![]() 与
与![]() 均为3的倍数.
均为3的倍数.
因此,![]() 被3整除.
被3整除.
因为![]() ,所以,
,所以,![]() 为合数.
为合数.
(2)已知![]() 不为2的倍数.则
不为2的倍数.则![]() 为奇数当且仅当
为奇数当且仅当![]() 、
、![]() 一个为奇数一个为偶数.
一个为奇数一个为偶数.
不妨设![]() 为奇数.则集合
为奇数.则集合![]() 的元素只能是
的元素只能是![]() 这1007个奇数.
这1007个奇数.
注意到,![]() .
.
在集合![]() 中含有因数31的数记为
中含有因数31的数记为![]() .
.
因为![]() 中含两个因数31,所以,集合
中含两个因数31,所以,集合![]() 中含因数31的共有34个.
中含因数31的共有34个.
从而,在集合![]() 中
中![]() 型的数中除去
型的数中除去![]() ,含有因数13的数超过34个.
,含有因数13的数超过34个.
类似地,在集合![]() 中
中![]() 型的数中除去
型的数中除去![]() 和
和![]() ,含有因数5的数远远超过34个.
,含有因数5的数远远超过34个.
于是,![]() .
.
集合![]() 的元素只能是
的元素只能是![]() 这1007个偶数.
这1007个偶数.
注意到,![]() .
.
在集合![]() 中含有因数31的数记为
中含有因数31的数记为
![]() .
.
因为![]() 中含两个因数31,所以,集合
中含两个因数31,所以,集合![]() 中含因数31的共有33个.
中含因数31的共有33个.
从而,在集合![]() 中
中![]() 型或
型或![]() 型的数含的因数5和13各自均多于33个.
型的数含的因数5和13各自均多于33个.
于是,![]() .
.
因此,![]() ,即
,即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】椭圆E: ![]() +
+ ![]() =1(a>b>0)的焦点到直线x﹣3y=0的距离为
=1(a>b>0)的焦点到直线x﹣3y=0的距离为 ![]() ,离心率为
,离心率为 ![]() ,抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点与E交于A,B,与G交于C,D.
,抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点与E交于A,B,与G交于C,D.
(1)求椭圆E及抛物线G的方程;
(2)是否存在学常数λ,使 ![]() 为常数,若存在,求λ的值,若不存在,说明理由.
为常数,若存在,求λ的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究钟表与三角函数的关系,以9点与3点所在直线为x轴,以6点与12点为y轴,设秒针针尖指向位置P(x,y),若初始位置为P0( ![]() ,
, ![]() ),秒针从P0(注此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t(秒)的函数关系为( )
),秒针从P0(注此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t(秒)的函数关系为( )
A.y=sin( ![]() t+
t+ ![]() )
)
B.y=sin( ![]() t﹣
t﹣ ![]() )
)
C.y=sin(﹣ ![]() t+
t+ ![]() )
)
D.y=sin(﹣ ![]() t﹣
t﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E. 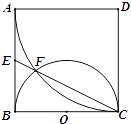
(1)求证:AE=EB;
(2)求EFFC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年,在国家创新驱动战略下,北斗系统作为一项国家高科技工程,一个开放型的创新平台,1400多个北斗基站遍布全国,上万台套设备组成星地“一张网”,国内定位精度全部达到亚米级,部分地区达到分米级,最高精度甚至可以达到厘米或毫米级。最近北斗三号工程耗资9万元建成一小型设备,已知这台设备从启用的第一天起连续使用,第![]() 天的维修保养费为
天的维修保养费为![]() 元,使用它直至“报废最合算”(所谓“报废最合算”是指使用这台仪器的平均每天耗资最少)为止,一共使用了多少天,平均每天耗资多少钱?
元,使用它直至“报废最合算”(所谓“报废最合算”是指使用这台仪器的平均每天耗资最少)为止,一共使用了多少天,平均每天耗资多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在长为10千米的河流![]() 的一侧有一条观光带,观光带的前一部分为曲线段
的一侧有一条观光带,观光带的前一部分为曲线段![]() ,设曲线段
,设曲线段![]() 为函数
为函数![]() (单位:千米)的图象,且图象的最高点为
(单位:千米)的图象,且图象的最高点为![]() ;观光带的后一部分为线段
;观光带的后一部分为线段![]() .
.
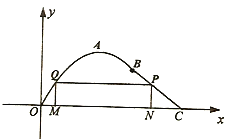
(1)求函数为曲线段![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)若计划在河流![]() 和观光带
和观光带![]() 之间新建一个如图所示的矩形绿化带
之间新建一个如图所示的矩形绿化带![]() ,绿化带仅由线段
,绿化带仅由线段![]() 构成,其中点
构成,其中点![]() 在线段
在线段![]() 上.当
上.当![]() 长为多少时,绿化带的总长度最长?
长为多少时,绿化带的总长度最长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com