Question

【题目】已知点及圆.

（1）若直线过点且被圆截得的线段长为，求的方程；

（2）求过点的圆的弦的中点的轨迹方程.

Answer 1

【答案】(1) 或；(2) .

【解析】试题分析：（1）直线与圆相交时，利用圆的半径，弦长的一半，圆心到直线的距离构成直角三角形的三边勾股定理求解；（2）求弦的中点的轨迹方程，首先设出动点坐标D（x，y），利用弦的中点与圆心的连线垂直于仙所在的直线得到动点的轨迹方程

试题解析：（1）解法一：如图所示，AB＝4，D是AB的中点，CD⊥AB，AD＝2，AC＝4，

在Rt△ACD中，可得CD＝2．

设所求直线的斜率为k，则直线的方程为y－5＝kx，

即kx－y＋5＝0．

由点C到直线AB的距离公式：

＝2，得k＝．

k＝时，直线l的方程为3x－4y＋20＝0．

又直线l的斜率不存在时，也满足题意，此时方程为x＝0．

∴所求直线的方程为3x－4y＋20＝0或x＝0．

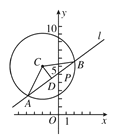
（2）设过P点的圆C的弦的中点为D（x，y），

则CD⊥PD，即

（x＋2，y－6）（x，y－5）＝0，化简得所求轨迹方程为x2＋y2＋2x－11y＋30＝0．