
【题目】已知函数f(x)= ![]() 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
A.(1,2)
B.(﹣1,0)
C.(﹣2,﹣1)
D.(﹣6,﹣1)
【答案】C
【解析】解:∵函数f(x)= ![]() 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,
图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,
而函数g(x)=kx+2e+1关于直线y=e的对称图象为y=﹣kx﹣1,
∴函数ff(x)= ![]() 图象与y=﹣kx﹣1的图象有且只有四个不同的交点,
图象与y=﹣kx﹣1的图象有且只有四个不同的交点,
作函数f(x)= ![]() 图象与y=﹣kx﹣1的图象如下,
图象与y=﹣kx﹣1的图象如下,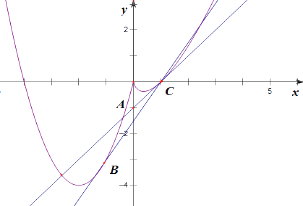 ,
,
易知直线y=﹣kx﹣1恒过点A(0,﹣1),
设直线AC与y=xlnx相切于点C(x,xlnx),
y′=lnx+1,
故lnx+1= ![]() ,
,
解得,x=1;
故kAC=1;
设直线AB与y=xlnx相切于点C(x,x2+4x),
y′=2x+4,
故2x+4= ![]() ,
,
解得,x=﹣1;
故kAC=﹣2+4=2;
故1<﹣k<2,
故﹣2<k<﹣1;
故选:C.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付![]() 又称手机支付
又称手机支付![]() 逐渐深入人民群众的生活
逐渐深入人民群众的生活![]() 某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对
某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对![]() 岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表
岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表![]() 部分数据模糊不清
部分数据模糊不清![]() 如表:
如表:
分组 | 频数 | 频率 | |
第1组 |
| 10 |
|
第2组 |
|
|
|
第3组 |
| 15 |
|
第4组 |
|
|
|
第5组 |
| 2 |
|
合计 | 50 |
| |
![]() 表中
表中![]() 处的数据分别是多少?
处的数据分别是多少?
![]() 从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
![]() 在
在![]() 抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB 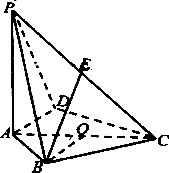
(1)求证:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值为2,求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,其右焦点到直线2ax+by﹣
,其右焦点到直线2ax+by﹣ ![]() =0的距离为
=0的距离为 ![]() .
.
(1)求椭圆C1的方程;
(2)过点P(0,﹣ ![]() )的直线l交椭圆C1于A,B两点.
)的直线l交椭圆C1于A,B两点.
①证明:线段AB的中点G恒在椭圆C2: ![]() +
+ ![]() =1的内部;
=1的内部;
②判断以AB为直径的圆是否恒过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,求对任意
分别是先后抛掷一枚骰子得到的点数,求对任意![]() ,
, ![]() 恒成立的概率;
恒成立的概率;
(2)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数, ![]() 是从
是从![]() 任取的一个数,求函数
任取的一个数,求函数![]() 的图像与
的图像与![]() 轴有交点的概率.
轴有交点的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com