
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)求椭圆标准方程,基本方法为待定系数法,即列两个独立条件![]() ,
,![]() 解出
解出![]() ,
,![]() (2)先化简等式:
(2)先化简等式:![]() 得
得![]() ,其中
,其中![]() 为线段
为线段![]() 的中点为,即所以直线
的中点为,即所以直线![]() 为直线
为直线![]() 的垂直平分线,直线
的垂直平分线,直线![]() 的垂直平分线过点
的垂直平分线过点![]() ,以下转化为中点弦问题,可利用韦达定理,也可利用点差法,得出t的函数解析式,根据对应参数(直线斜率或中点坐标)的取值范围确定实数
,以下转化为中点弦问题,可利用韦达定理,也可利用点差法,得出t的函数解析式,根据对应参数(直线斜率或中点坐标)的取值范围确定实数![]() 的取值范围
的取值范围
试题解析:(1)由题意知![]() ,又
,又![]() ,所以
,所以![]() ,
,
![]() ,所以椭圆的方程为:
,所以椭圆的方程为:![]() ;
;
(2)设直线![]() 的方程为:
的方程为:![]() ,代入
,代入![]() ,得:
,得:
![]() ,设
,设![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,
则![]() ,
,
由![]() 得:
得:![]() ,
,
所以直线![]() 为直线
为直线![]() 的垂直平分线,
的垂直平分线,
直线![]() 的方程为:
的方程为:![]() ,
,
令![]() 得:
得:![]() 点的横坐标
点的横坐标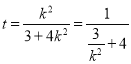 ,
,
因为![]() , 所以
, 所以![]() ,所以
,所以![]() .
.
所以线段![]() 上存在点
上存在点![]() 使得
使得![]() ,其中
,其中![]() .
.


科目:高中数学 来源: 题型:
【题目】50.6,0.65,log0.55的大小顺序是( )
A.0.65 < log0.65 < 50.6B.0.65 < 50.6< log0.65
C.log0.65 < 50.6 <0.65D.log0.65 <0.65 < 50.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直,
其中真命题是( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明当n∈N*时,1+2+22+…+25n-1是31的倍数时,当n=1时原式为( )
A. 1 B. 1+2
C. 1+2+3+4 D. 1+2+22+23+24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李参加一种红包接龙游戏:他在红包里塞了12元,然后发给朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 将获得红包里的所有金额;如果
将获得红包里的所有金额;如果![]() 未猜中,
未猜中,![]() 将当前的红包转发给朋友
将当前的红包转发给朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 平分红包里的金额;如果
平分红包里的金额;如果![]() 未猜中,
未猜中,![]() 将当前的红包转发给朋友
将当前的红包转发给朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 和
和![]() 平分红包里的金额;如果
平分红包里的金额;如果![]() 未猜中,红包里的钱将退回小李的账户,设
未猜中,红包里的钱将退回小李的账户,设![]() 猜中的概率分别为
猜中的概率分别为![]() ,且
,且![]() 是否猜中互不影响.
是否猜中互不影响.
(1)求![]() 恰好获得4元的概率;
恰好获得4元的概率;
(2)设![]() 获得的金额为
获得的金额为![]() 元,求
元,求![]() 的分布列;
的分布列;
(3)设![]() 获得的金额为
获得的金额为![]() 元,
元,![]() 获得的金额为
获得的金额为![]() 元,判断
元,判断![]() 所获得的金额的期望能否超过
所获得的金额的期望能否超过![]() 的期望与
的期望与![]() 的期望之和.
的期望之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com