
����Ŀ�����Ż������ķ�չ���ƶ�֧��![]() �ֳ��ֻ�֧��
�ֳ��ֻ�֧��![]() ����������Ⱥ�ڵ�����
����������Ⱥ�ڵ�����![]() ijѧУ��ȤС��Ϊ���˽��ƶ�֧��������Ⱥ���е���֪�ȣ���
ijѧУ��ȤС��Ϊ���˽��ƶ�֧��������Ⱥ���е���֪�ȣ���![]() �����Ⱥ����������飬��������������ʹ���ƶ�֧���������У��ش��������Ĺ���50���ˣ�����50���˰�������ֳ�5�飬�����Ƴ�Ƶ�ʷֲ���
�����Ⱥ����������飬��������������ʹ���ƶ�֧���������У��ش��������Ĺ���50���ˣ�����50���˰�������ֳ�5�飬�����Ƴ�Ƶ�ʷֲ���![]() ��������ģ������
��������ģ������![]() �����
�����
���� | Ƶ�� | Ƶ�� | |
��1�� |
| 10 |
|
��2�� |
|
|
|
��3�� |
| 15 |
|
��4�� |
|
|
|
��5�� |
| 2 |
|
�ϼ� | 50 |
| |
![]() ����
����![]() �������ݷֱ��Ƕ��٣�
�������ݷֱ��Ƕ��٣�
![]() �ӵ�1�飬��3�飬��4�����÷ֲ�����ķ�����ȡ6�ˣ���ÿ���ȡ��������
�ӵ�1�飬��3�飬��4�����÷ֲ�����ķ�����ȡ6�ˣ���ÿ���ȡ��������
![]() ��
��![]() ��ȡ��6�����������ȡ2�ˣ�������ȡ��2������ͬһ����ĸ��ʣ�
��ȡ��6�����������ȡ2�ˣ�������ȡ��2������ͬһ����ĸ��ʣ�
���𰸡���1������������2������������3��![]()
��������
![]() ��Ƶ�ʷֲ������������
��Ƶ�ʷֲ������������![]() �������ݣ�
�������ݣ�![]() �ӵ�1�飬��3�飬��4�����÷ֲ�����ķ�����ȡ6�ˣ��ɵ�1�飬��3�飬��4�������֮��Ϊ10��15��
�ӵ�1�飬��3�飬��4�����÷ֲ�����ķ�����ȡ6�ˣ��ɵ�1�飬��3�飬��4�������֮��Ϊ10��15��![]() ��3��1������������
��3��1������������![]() ��ӵ�1���ȡ��2��Ϊ
��ӵ�1���ȡ��2��Ϊ![]() ��
��![]() ���ӵ�3���ȡ��3��Ϊ
���ӵ�3���ȡ��3��Ϊ![]() ��
��![]() ��
��![]() ���ӵ�4���ȡ��1��ΪC������6���������ȡ2�ˣ������оٷ����������ȡ��2������ͬһ����ĸ��ʣ�
���ӵ�4���ȡ��1��ΪC������6���������ȡ2�ˣ������оٷ����������ȡ��2������ͬһ����ĸ��ʣ�
![]() ��Ƶ�ʷֲ����ã�
��Ƶ�ʷֲ����ã�
![]() ����������1��
����������1��![]() ���������ǣ�
���������ǣ�![]() ��
��
![]() ���������ǣ�
���������ǣ�![]() ��
��
![]() ���������ǣ�
���������ǣ�![]() ��
��
![]() ���������ǣ�
���������ǣ�![]() ��
��
![]() ��1�飬��3�飬��4�������֮��Ϊ��
��1�飬��3�飬��4�������֮��Ϊ��
10��15��![]() ��3��1��
��3��1��
![]() �ӵ�1���ȡ������Ϊ��
�ӵ�1���ȡ������Ϊ��![]() �ˣ�
�ˣ�
�ӵ�3���ȡ������Ϊ��![]() �ˣ�
�ˣ�
�ӵ�4���ȡ������Ϊ��![]() �ˣ�
�ˣ�
![]() ��ӵ�1���ȡ��2��Ϊ
��ӵ�1���ȡ��2��Ϊ![]() ��
��![]() ���ӵ�3���ȡ��3��Ϊ
���ӵ�3���ȡ��3��Ϊ![]() ��
��![]() ��
��![]() ���ӵ�4���ȡ��1��ΪC��
���ӵ�4���ȡ��1��ΪC��
�����6���������ȡ2�ˣ������¼���15�����ֱ�Ϊ��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
����ȡ��2������ͬһ��������Ļ����¼���4�����ֱ�Ϊ��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ����ȡ��2������ͬһ����ĸ���
����ȡ��2������ͬһ����ĸ���![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����з��д�С����״��ͬ��С�����ɣ����б��Ϊ0��С��1�������Ϊ1��С��1�������Ϊ2��С��![]() ��.���Ӵ����������ȡ1��С��ȡ�����Ϊ2��С��ĸ�����
��.���Ӵ����������ȡ1��С��ȡ�����Ϊ2��С��ĸ�����![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2���Ӵ������зŻص������ȡ2��С�ǵ�һ��ȡ����С����Ϊ![]() ���ڶ���ȡ����С����Ϊ
���ڶ���ȡ����С����Ϊ![]() .
.
�ټǡ�![]() ��Ϊ�¼�
��Ϊ�¼�![]() �����¼�
�����¼�![]() �ĸ��ʣ�
�ĸ��ʣ�
��������![]() ����ȡ2��ʵ��
����ȡ2��ʵ��![]() �����¼���
�����¼���![]() ��������ĸ���.
��������ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����ͼ����[a��b]���������ϣ����壺
f1��x��=min{f��t��| a��t��x}��x��[a��b]����
f2��x��=max{f��t��| a��t��x}��x��[a��b]����
���У�min{f��x��| x��D}��ʾ����f��x����D�ϵ���Сֵ��max{f��x��|x��D}��ʾ����f��x����D�ϵ����ֵ����������С������k��ʹ��f2��x��-f1��x����k��x-a���������x��[a��b]��������ƺ���f��x��Ϊ[a��b]�ϵġ�k��������������
��1����f��x��=sinx��x��[![]() ��
�� ![]() ]����ֱ��д��f1��x����f2��x���ı���ʽ��
]����ֱ��д��f1��x����f2��x���ı���ʽ��
��2����֪����f��x��=��x-1��2��x��[-1��4]�����ж�f��x���Ƿ�Ϊ[-1��4]�ϵġ�k������������������ǣ������Ӧ��k��������ǣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС�����о���ҹ�²��С�뻼��ð��������֮��Ĺ�ϵ,���Ƿֱ��������ijҽԺ��¼�� 1��6�·�ÿ��10�ŵ���ҹ�²��������ð��������������õ��������ϣ�
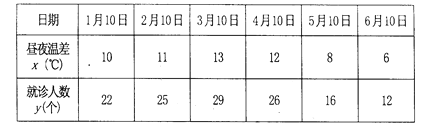
����ȤС��ȷ�����о������ǣ�����2��3��4��5�µ�4�����������Իع鷽�̣�����1�º�6�µ�2�����ݽ��м���.
��1�������2��3��4��5�µ����ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2���������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2�ˣ�����Ϊ�õ������Իع鷽��������ģ����ʸ�С���������Իع鷽���Ƿ����룿
���ο���ʽ�� 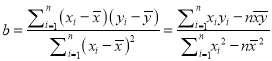 ��
�� ![]() ��
��
�ο����ݣ� ![]() ��
��
![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ�ڽ�������һ���ڼ��У�����н��Ұ�װ��ͬһ�ͺŵĿյ������������յ���ʹ������![]() ��λ����
��λ����![]() ����֧����ά������
����֧����ά������![]() ��λ��ǧԪ
��λ��ǧԪ![]() �����ṩ��ͳ�����������
�����ṩ��ͳ�����������
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
![]() ��x��y֮����������ع�ϵ�������ά������y����x�����Իع�ֱ�߷���
��x��y֮����������ع�ϵ�������ά������y����x�����Իع�ֱ�߷���![]() ��
��
![]() ���涨��ά������y����
���涨��ά������y����![]() ǧԪʱ�������յ����뱨�ȣ��Ը���
ǧԪʱ�������յ����뱨�ȣ��Ը���![]() �Ľ���������յ�ʹ���������ֵ
�Ľ���������յ�ʹ���������ֵ![]() ���ȡ����
���ȡ����![]() �ο���ʽ��
�ο���ʽ��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ͼ�������ҽ����ĸ���ͬ�ĵ����ֱ��y=e�ĶԳƵ��ں���g��x��=kx+2e+1��ͼ���ϣ���ʵ��k��ȡֵ��ΧΪ�� ��
ͼ�������ҽ����ĸ���ͬ�ĵ����ֱ��y=e�ĶԳƵ��ں���g��x��=kx+2e+1��ͼ���ϣ���ʵ��k��ȡֵ��ΧΪ�� ��
A.��1��2��
B.����1��0��
C.����2����1��
D.����6����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���֪��![]() ��
��![]() ��ԲC�ķ���Ϊ
��ԲC�ķ���Ϊ![]() ����PΪԲ�ϵĶ��㣮
����PΪԲ�ϵĶ��㣮
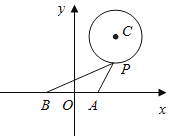
![]() �����A��ԲC�����߷��̣�
�����A��ԲC�����߷��̣�
![]() ��
��![]() �����ֵ����ʱ��Ӧ�ĵ�P�����꣮
�����ֵ����ʱ��Ӧ�ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڷ���ʵ�����ϵĺ���![]() ����
����![]() ����
����![]() ������
������![]() �ϵĵ���������
�ϵĵ���������
��1����![]() ��ֵ��
��ֵ��
��2����֤�� ![]() ��
��
��3���ⲻ��ʽ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �����Σ�
������ ![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ����
����![]() �ϵ�һ���㣬
�ϵ�һ���㣬 ![]() ��
�� ![]() Ϊ
Ϊ![]() ���е�.
���е�.
��1��֤���� ![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com