练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题，规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格。

    （1）分别求甲、乙两人考试合格的概率；

    （2）求甲、乙两人至少有一人考试合格的概率。



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知点是直线上一动点，是圆：的两条切线，为切点，若四边形的最小面积是2，则的值为（   ）

    A．4              B．          C．2            D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图11-19，在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=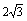，M、N分别为AB、SB的中点

    （1）证明：AC⊥SB；

    （2）求二面角N-CM-B的大小。

    （3）求点B到平面CMN的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知空间三点A(0,2,3)，B(－2,1,6)，C(1，－1,5)．则以，为边的平行四边形的面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱柱ABC-A1B1C1中，A1在底面上的射影在线段AC上，底面△ABC是以∠B为直角的等腰三角形，M为AC的中点，又AB=AA1=a

    （1）求证：BM⊥AA1；

    （2）若A1C⊥平面BMC1，求证：三棱柱ABC-A1B1C1为直三棱柱。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一接等中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的概率为0.5，电话C、D战线的概率为0.4，各部电话是否占线相互之间没有影响，假设该时刻有ξ部电话占线，试求随机变量ξ的概率分布和它的期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


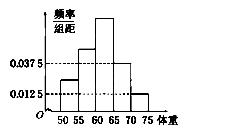
    如图是某学校学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率之比为1∶2∶3，第2小组的频数为10，则抽取的学生人数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    袋中有个白球和个黑球，每次从中任取个球，每次取出黑球后不再放回去，直到取出白球为止．求取球次数的分布列，并求出的期望值和方差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在数列{an}、{bn}中，a1＝2，b1＝4，且an，bn，an＋1成等差数列，bn，an＋1，bn＋1成等比数列(n∈N*)．

    求a2，a3，a4及b2，b3，b4，由此猜测{an}、{bn}的通项公式，并证明你的结论；（用数学归纳法证明）

    查看答案和解析>>

    同步练习册答案