
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,在直角梯形
,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点
的中点
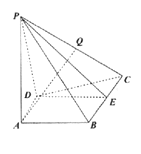
(1)求证:平面![]() 平面
平面![]()
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由
的位置;若不存在,请说明理由
(3)若![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】若数列![]() 的前
的前![]() 项和为
项和为![]() ,则下列命题:(1)若数列
,则下列命题:(1)若数列![]() 是递增数列,则数列
是递增数列,则数列![]() 也是递增数列;(2)数列
也是递增数列;(2)数列![]() 是递增数列的充要条件是数列
是递增数列的充要条件是数列![]() 的各项均为正数;(3)若
的各项均为正数;(3)若![]() 是等差数列(公差
是等差数列(公差![]() ),则
),则![]() 的充要条件是
的充要条件是![]() ;(4)若
;(4)若![]() 是等比数列,则
是等比数列,则![]() 的充要条件是
的充要条件是![]() .其中,正确命题的个数是( )
.其中,正确命题的个数是( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的导函数为f′(x),若f(x)=![]() ex﹣f(0)x+
ex﹣f(0)x+![]() x2(e是自然对数的底数).
x2(e是自然对数的底数).
(1)求f(0)和f′(1)的值;
(2)若g(x)=![]() x2+a与函数f(x)的图象在区间[﹣1,2]上恰有2两个不同的交点,求实数a的取值范围.
x2+a与函数f(x)的图象在区间[﹣1,2]上恰有2两个不同的交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
![]()
(1)请根据表中提供的数据,用相关系数![]() 说明
说明![]() 与
与![]() 的线性相关程度;(结果保留小数点后两位,参考数据:
的线性相关程度;(结果保留小数点后两位,参考数据: ![]() )
)
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式: ,
,![]() ;相关系数
;相关系数 ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有初级教师21人,中级教师14人,高级教师7人,现采用分层抽样的方法从这些教师中抽取6人对绩效工资情况进行调查.
(1)求应从初级教师,中级教师,高级教师中分别抽取的人数;
(2)若从抽取的6名教师中随机抽取2名做进一步数据分析,求抽取的2名均为初级教师的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是( ) 
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产能利用率是指实际产出与生产能力的比率,工r产能利用率是衡量工业生产经营状况的重要指标.下图为国家统计局发布的2015年至2018年第2季度我国工业产能利用率的折线图.
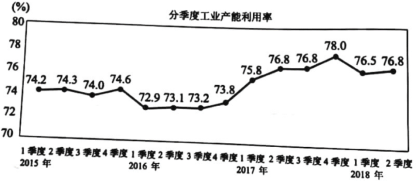
在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2016年第二季度与2015年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2015年第二季度与2015年第一季度相比较.
据上述信息,下列结论中正确的是( ).
A. 2015年第三季度环比有所提高B. 2016年第一季度同比有所提高
C. 2017年第三季度同比有所提高D. 2018年第一季度环比有所提高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() :
: ![]() 的上、下焦点,
的上、下焦点, ![]() 是抛物线
是抛物线![]() :
: ![]() 的焦点,点
的焦点,点![]() 是
是![]() 与
与![]() 在第二象限的交点,且
在第二象限的交点,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)与圆![]() 相切的直线
相切的直线![]() :
: ![]() (其中
(其中![]() )交椭圆
)交椭圆![]() 于点
于点![]() ,
, ![]() ,若椭圆
,若椭圆![]() 上一点
上一点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com