
 ,
, 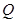 为底面圆周上一点.
为底面圆周上一点.
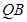 的中点为
的中点为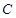 ,
,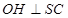 ,求证
,求证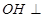 平面
平面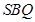 ;
;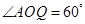 ,
,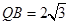 ,求此圆锥的全面积.
,求此圆锥的全面积.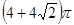 .
.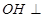 平面
平面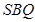 ,即证
,即证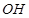 垂直于平面内的两条相交直线,
垂直于平面内的两条相交直线,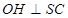 是已知,转化为证
是已知,转化为证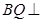 平面
平面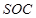 ,利用母线相等,利用底面半径相等,
,利用母线相等,利用底面半径相等,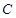 为中点,证得
为中点,证得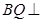 平面
平面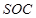 ,证得,
,证得,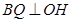 ,得证;(2)
,得证;(2)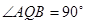 ,求出底面半径,以及母线长,根据全面积公式,
,求出底面半径,以及母线长,根据全面积公式,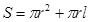 ,求出全面积.
,求出全面积. 平面ABQ
平面ABQ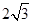 ,∴直角△ABQ中,∠ABQ=30°,
,∴直角△ABQ中,∠ABQ=30°,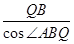 =4 8分
=4 8分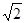 ,
,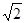 =4
=4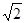 π 10分
π 10分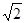 π+π×22=(4+4
π+π×22=(4+4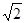 )π 12分
)π 12分

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:解答题
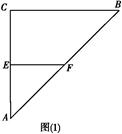
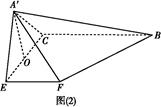
 A′BC的体积.
A′BC的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com