选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
的参数方程为
（
为参数），以坐标原点
为极点，以
轴正半轴为极轴，建立极坐标系，圆
的极坐标方程为
．
（Ⅰ）求的普通方程和的直角坐标方程；
（Ⅱ）设点
为曲线上任意一点，过作圆的切线，切点为
，求
的最小值．
备战中考寒假系列答案科目：高中数学 来源：2017届湖南省、衡阳八中等十三校重点中学第一次联考数学（文）试卷（解析版） 题型：选择题
复数
(
为虚数单位)在复平面内对应的点在（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目：高中数学 来源：2017届广东省广州市高三3月综合测试（一）数学理试卷（解析版） 题型：选择题
若直线
与函数
的图象相交于点
，
，且
，则线段
与函数
的图象所围成的图形面积是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2017届河南省安阳市高三第二次模拟考试数学（理）试卷（解析版） 题型：解答题
设数列
的前
项和为
，满足
，
．
（Ⅰ）求的通项公式；
（Ⅱ）设
，数列
的前项和为
，求数列
的前项和．
查看答案和解析>>
科目：高中数学 来源：2017届河南省安阳市高三第二次模拟考试数学（理）试卷（解析版） 题型：选择题
北宋数学家沈括的主要数学成就之一为隙积术，所谓隙积，即“积之有隙”者，如果棋、层坛之类，这种长方台形状的物体垛积.设隙积共
层，上底由
个物体组成，以下各层的长、宽一次各增加一个物体，最下层（即下底）由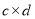
个物体组成，沈括给出求隙积中物体总数的公式为
.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示，则该垛积中所有小球的个数为（ ）
A. 83 B. 84 C. 85 D. 86
查看答案和解析>>
科目：高中数学 来源：2017届河南省焦作市高三下学期第二次模拟考试数学（文）试卷（解析版） 题型：解答题
已知圆
： 
过椭圆
： 
(
)的短轴端点， 
， 
分别是圆
与椭圆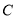
上任意两点，且线段
长度的最大值为3．
（Ⅰ）求椭圆
的方程；
（Ⅱ）过点
作圆
的一条切线交椭圆
于
， 
两点，求
的面积的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则该曲线的普通方程为
B. 
C. 
D. 
, 则输出
的值为. 
B．
C．
D．
图1
，则
__________．